On September 14, a research team led by Associate Professor Guixin Li (Materials Science and Engineering) and the Université de Bordeaux Professor Etienne Brasselet published cutting-edge research findings. Their findings provide a novel scheme for generating spin-orbit angular momentum of nonlinear optical waves through a cascade process. Their paper, titled “Harmonic spin-orbit angular momentum cascade in nonlinear optical crystals,” was published in the high-impact academic journal, Nature Photonics (IF = 31.5).
Almost three decades after optical beam with helical phase profiles have been identified as carrying a well-defined orbital angular momentum (OAM) per photon, the efforts for the generation and control of single or multiple OAM states is ever-increasing. This trend is nurtured by the advent of spin-controlled photonics, which sets the polarization state of light as an independent degree of freedom to tailor the optical spatial degrees of freedom.
The development of technologies enabling spin-controlled OAM states has started in the 2000s in the framework of linear optics with the emergence of devices made of (i) homogeneous anisotropic materials, (ii) structured isotropic materials, and (iii) structured anisotropic materials. Nowadays, it is option (ii) that attracts most research developments following the demonstration of spin-controlled OAM generation in the visible regime by geometric phase metasurfaces.
Meanwhile, textbook wave-mixing processes from homogeneous crystals have been extended to fields carrying OAM since the 1990s and later to 2D and 3D structured nonlinear photonic crystals for the production of harmonic OAM states by design. Again, option (ii) imposes itself as a versatile approach merging optical spin-orbit coupling with nonlinear optics.
Here the authors revisit the longstanding spin-selective second-harmonic wave (SHW) generated by a circularly polarized fundamental wave (FW) along the optical axis of a crystal with three-fold rotational symmetry in the realm of spin-orbit nonlinear wave-mixing.
They show that multiple spin-orbit optical states can be generated without the need for artificial structuring of photonic properties or non-paraxial regime. This outcome contrasts with all experimental studies carried out so far in the paraxial regime. How the spin-orbit content of an FW carrying non-zero OAM is transformed into the SHW, however, remains unexplored yet and sets of the starting point of our study.
Optical angular momentum-based photonic technologies pinpoint the critical role of optical spin-orbit interaction. It usually implies spatially engineered optical materials and linear optical phenomena. By re-assessing nonlinear optics of homogeneous crystals under circularly polarized light, the authors reported on the enrichment of the spin-orbit angular momentum spectrum of the paraxial light.
They demonstrated it in the framework of the second harmonic generation using a crystal with three-fold rotational symmetry. Four spin-orbit optical states for the second harmonic field are predicted from a single fundamental one owing to the interplay between linear spin-orbit coupling and nonlinear wave mixing, three of them being experimentally ascertained.
Their findings suggest that the fundamentals of nonlinear optics are worth revisiting through the prism of the spin-orbit interaction of light. They also represent a spin-controlled nonlinear route to orbital angular multiplexing, modal vortex light sources, high-dimensional parametric processes, and multi-state optical magnetization.
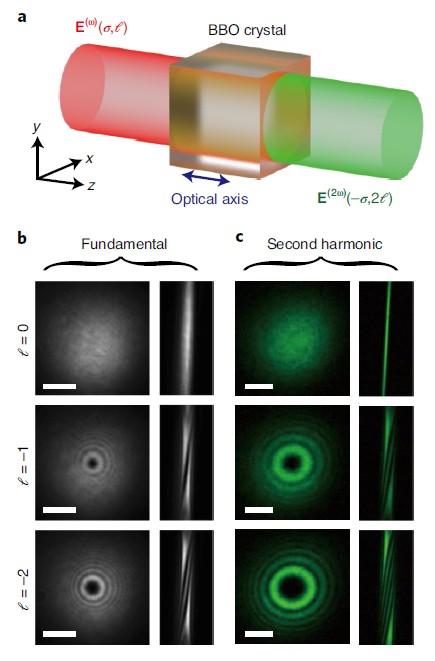
Figure 1 Spin-selective second harmonic generation along the optical axis of a BBO crystal. A) Light-matter interaction geometry when the nonlinear crystal is pumped by a collimated fundamental wave (red) with an angular momentum state of (σ, ℓ)ω that generates a second harmonic wave (green) with an angular momentum state of (−σ, 2ℓ)2ω. B) Left/right column: intensity profiles of the fundamental wave at the mid-plane of the crystal imaged using a spherical/cylindrical lens for (σ, ℓ)ω=(+1, 0), (+1, 1) and (+1, 2). C) Left/right column: intensity profiles of the generated second-harmonic waves with angular momentum states of (−1, 0)2ω, (−1, −2)2ω, and (−1, −4)2ω imaged at the mid-plane of the crystal using a spherical/cylindrical lens. Scale bar: 1 mm
The experimental configuration is illustrated in Figure 1A. The research group introduced the spin-orbit optical states of the fundamental and the harmonic waves as optical states, where refers to the photon helicity that is related to left/right-handed circularly polarization states defined by the unit vectors and ℓ integer refers to the topological charge of on-axis optical phase singularity associated with a complex field amplitude where is the polar angle in the (x, y) transverse plane.
The experiment is carried out by irradiating a 5 mm-thick c-cut β-BaB2O4 (BBO) crystal with a femtosecond laser source at 1070 nm propagating along the optical axis of the crystal.
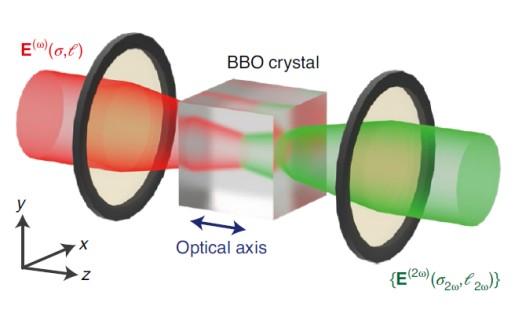
Figure 2 Spin-orbit angular momentum cascade during second harmonic generation along the optical axis of a BBO crystal for weakly focused pumping light. Illustration of the light-matter interaction geometry. The fundamental wave with angular momentum state of (σ, ℓ) generates a second-harmonic field constituted of as a set of distinct angular momentum states (σ2ω, ℓ2ω).
The spin-orbit content of the SHW drastically enriches as soon as the linear spin-orbit coupling process inherent to the propagation of focused light along the optical axis takes place (Figure 2).
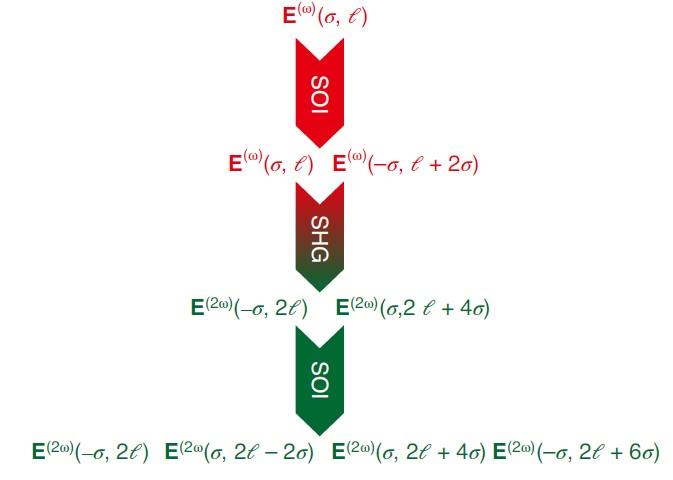
Figure 3 Three-step description of the spin-orbit angular momentum cascade for a second-harmonic generation along the optical axis of a nonlinear crystal with three-fold rotational symmetry. The first step of the process is the generation of the state (−σ, ℓ+2σ)ω via linear the spin-orbit coupling experienced by the fundamental wave. The second step is the second-harmonic generation itself. It relies on the nonlinear optics selection rules of circular polarization state and the conservation law for the orbital angular momentum per photon, leads to states (−σ, 2ℓ)2ω and (σ, 2ℓ+4σ)2ω. The third step corresponds to linear spin-orbit coupling experienced by each of the circularly polarized components of the second-harmonic field, which produces the states (σ, 2ℓ−2σ)2ω and (−σ, 2ℓ+6σ)2ω.
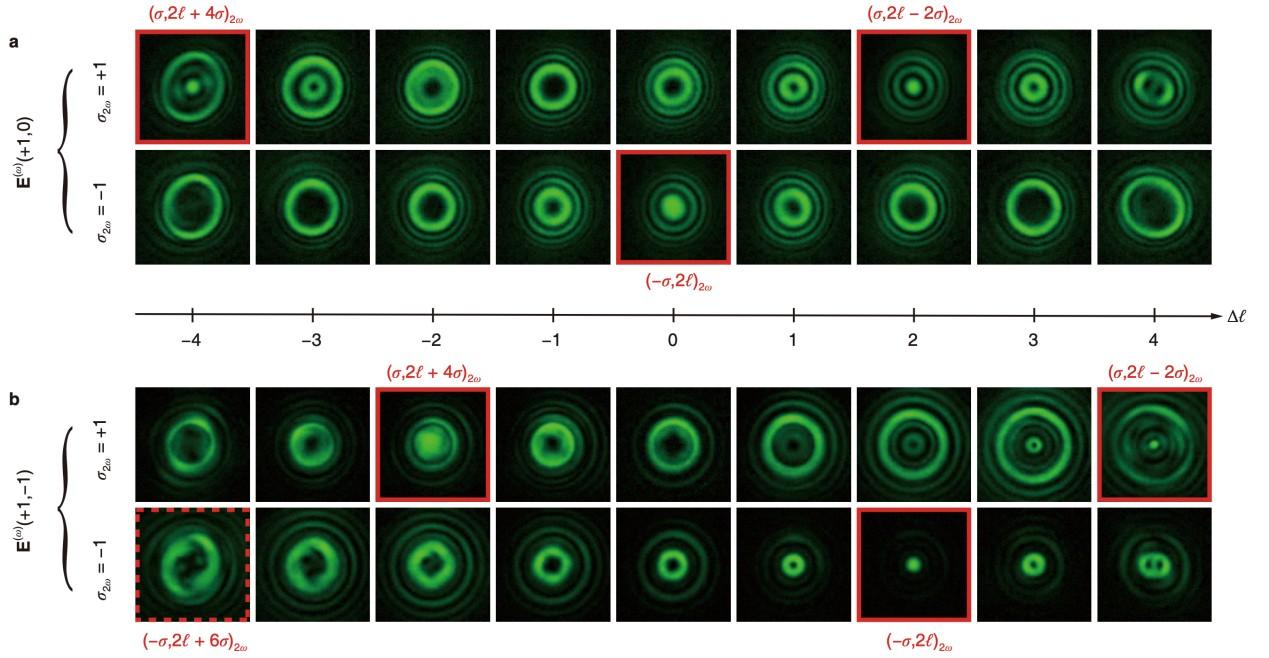
Figure 4 Spin-orbit tomography of the second-harmonic field during second harmonic generation along the optical axis of a BBO crystal for weakly focused pumping light. The spin-orbit optical content of the second harmonic field is retrieved by imparting a set of helical phase profiles with topological charge Δℓ to each of the circularly polarized field components. It uses a set of azimuthally-varying half-wave plates followed by an optical Fourier transform performed by a spherical lens. A) The incident fundamental optical state is (σ, ℓ)ω = (+1, 0). Three over four angular momentum states (−1, 0)2ω, (+1, +4)2ω and (+1, −2)2ω are identified as on-axis intensity spot (see red boxes). The fourth falls outside the experimentally accessible OAM range. B) The incident fundamental optical state is (σ, ℓ)ω = (+1, −1). Three over four angular momentum states (−1, −2)2ω, (+1, +2)2ω, and (+1, −4)2ω are identified (see red solid line boxes). The fourth predicted state is not observed (see red dashed line box).
The results are shown in Figure 4A for an incident Gaussian FW with the state . The latter limited bandwidth for deciphering the OAM spectrum is enough to recover all the predicted states in the particular case , whose results are shown in Figure 4B for incident FW state Despite careful optical settings, the is not found.
Nevertheless, the observed broken axisymmetry that is all the more pronounced as increases, which is consistent with helical phase masks imperfections, could explain the difficulty to unravel experimentally the state that is “at the end” of the harmonic spin-orbit angular momentum cascade (see Figure 3).
The interplay between the spin-orbit coupling and nonlinear wave-mixing in the framework of second-harmonic generation and crystals with C3v symmetry can be extended to high-harmonic (HH) processes and other discrete rotational symmetries. Circular polarization selection rules have been previously established for non-zero OAM and in the absence of spin-orbit interaction mediated by the optical anisotropy.
Extending these results to the non-paraxial is a task for future studies. The practical outcomes of this research would be to reach phase-matching conditions and ensuring drastically higher efficient harmonic generation. Another option to increase efficiency could be to implement a single pass quasi-phase-matching process or an intra-cavity design. Either way, the rich physics observed in this work shows that the re-examination of nonlinear optical processes in crystals is worth considering.
The flat-optics version of the present work seems possible, given that the long-established selection rules about circular polarization states of harmonic generation in bulk crystals also apply to 2D metacrystals. It could be done by multiplexing nonlinear and multiple-wavelength spin-orbit features into a single metadevice. These results also open possible avenues for controlling the multiplexed angular momentum states of light, which may have important applications in areas such as high dimensional quantum information processing, optical pulses with frequency-dependent OAM, and multi-state optical magnetization.
SUSTech Ph.D. student Yutao Tang and Dr. Kingfai Li are the co-first authors of the paper. Dr. Guixin Li and the Université de Bordeaux Prof. Etienne Brasselet are the co-correspondent authors. SUSTech Dr. Junhong Deng from Shenzhen Institute for Quantum Science and Engineering and Ph.D. student Xuecai Zhang from the Department of Materials Science and Engineering also made vital contributions to this study.
This work is supported by the National Natural Science Foundation of China, the Guangdong Provincial Innovation and Entrepreneurship Project, and the Qiu Shi Science & Technologies Foundation.
Proofread ByYingying XIA
Photo ByDepartment of Materials Science and Engineering, Yan QIU