Recently, the research group of Associate Professor Qihang Liu of the Department of Physics at the Southern University of Science and Technology (SUSTech) has made substantial progress in the field of magnetic topological materials. Their research results were recently published in the top journal Nature Communications, entitled “Spectral signatures of the surface anomalous Hall effect in magnetic axion insulators.”

The special electronic boundary state behavior is the unique property of topological materials such as topological insulators, Weyl semimetals, axion insulators, and topological superconductors. The observation is generally regarded as one of the direct pieces of evidence to confirm the topological properties of materials. Closely related to this is the transport property of the material in the measurement, which is the so-called “quantum anomalous Hall effect.” The theory shows that the surface of magnetic topological materials holds a half-integer quantized quantum anomalous Hall conductance (σ_xy=0.5 e^2/h), which is considered to be the boundary representation of the bulk topological magnetoelectric effect. Because the boundary state and quantum anomalous Hall effect are insensitive to the influence of impurities, defects, and other perturbations, they show high prospective in the design of low-dissipation electronic devices and quantum computing devices, which attracts widespread attention in recent decades.

The rise of the topological material MnBi2Te4/(Bi2Te3)n with intrinsic magnetization provides an excellent platform for studying axion insulators with broken time-reversal symmetry. Previous theoretical research from the team has shown that changing the ratio of MnBi2Te4 and Bi2Te3 layers in the material and their stacking sequence through material design can achieve a variety of topological phases, including time-reversal symmetric quantum spin Hall effect, time-reversal symmetry broken quantum spin Hall effect, as well as the quantum anomalous Hall effect.

In this research, the group further explored the relationship between the appearance of different topological phases and the strength of electronic transitions and exchange interactions in materials. After establishing the effective model Hamiltonian by adjusting the parameters in the model, the materials can be controlled to reach different topology phases such as axion insulators, Weyl semimetals, three-dimensional Chern insulators, three-dimensional quantum spin Hall insulators (fragile topology), etc. These are shown in the image below (Figure 1). Such an abundant topological quantum phase diagram greatly expands the potential application prospects of the Mn-Bi-Te system.

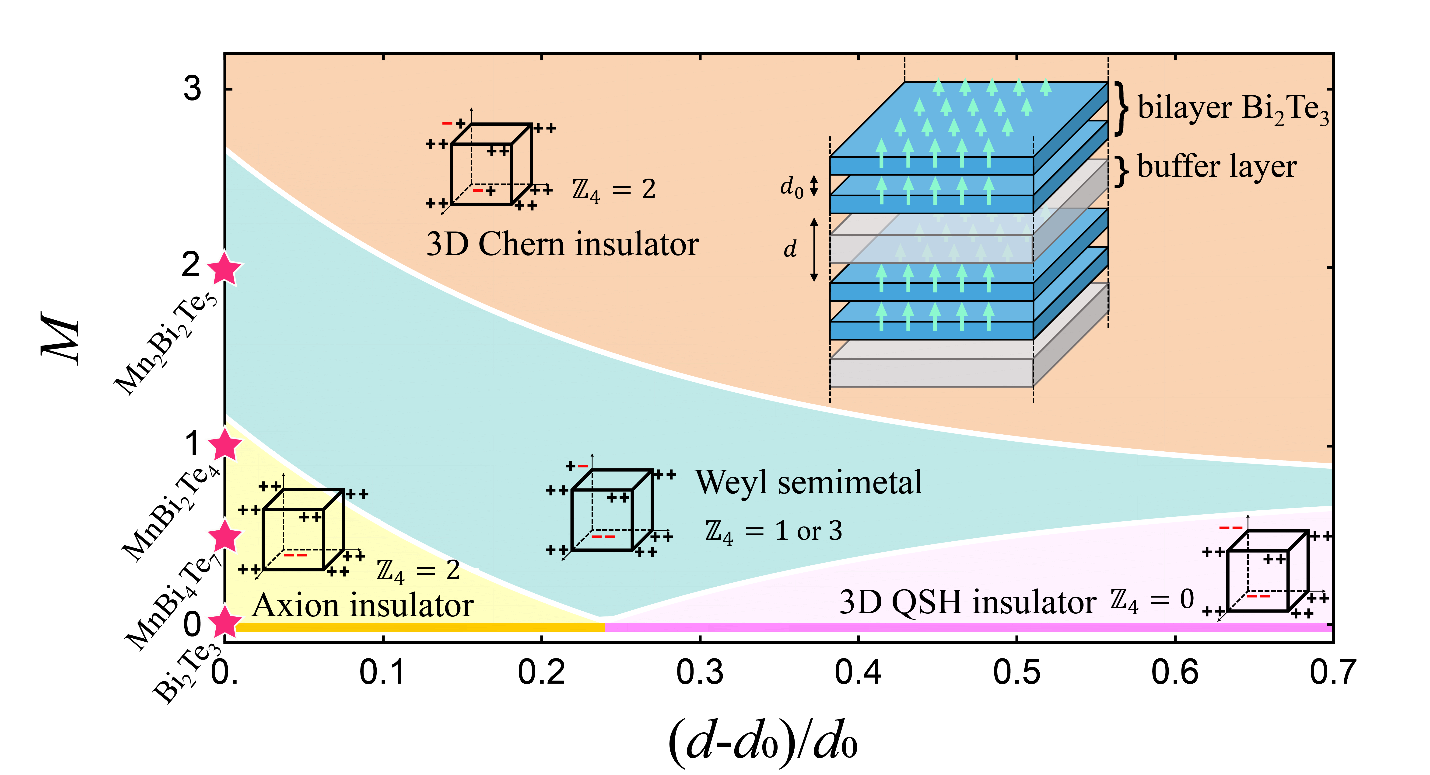
Figure 1. Abundant topological quantum phase diagram predicted by varying the inter-bilayer electron hopping and the strength of electron exchange.

The above-mentioned abundant phase diagram provides an excellent platform for studying the behavior of electronic edge states under different topological phases. The topological phases correspond to special edge states, including two-dimensional surface states (SS), one-dimensional edge states (hinge states, HS), and zero-dimensional corner states (CS). The theoretical analysis predicts that HS should be present at the edge of the surface of the ferromagnetic axion insulator, yet not in the antiferromagnetic axion insulator. It is necessary to study and analyze the specific behaviors and experimental measurables in this system from the perspective of atomistic simulation.

Qihang Liu’s research group developed a method based on density functional first-principles calculations to calculate the atomic layer-resolved local anomalous Hall conductance and boundary state electron energy spectra. Simulations of MnBi2Te4/(Bi2Te3)n in different quantum states show that the axion insulators MnBi2Te4 and MnBi4Te7 in the ferromagnetic or antiferromagnetic state exhibit half-integer quantized anomalous Hall conductance on the surface. The observable physical quantity corresponding to such a half-integer quantization effect is the key for experimentalists. To push forward the study, the group calculated the electronic state energy spectrum at the upper and lower surfaces, side surfaces, and edges of the material by using Green’s function method, as shown below (Figure 2).

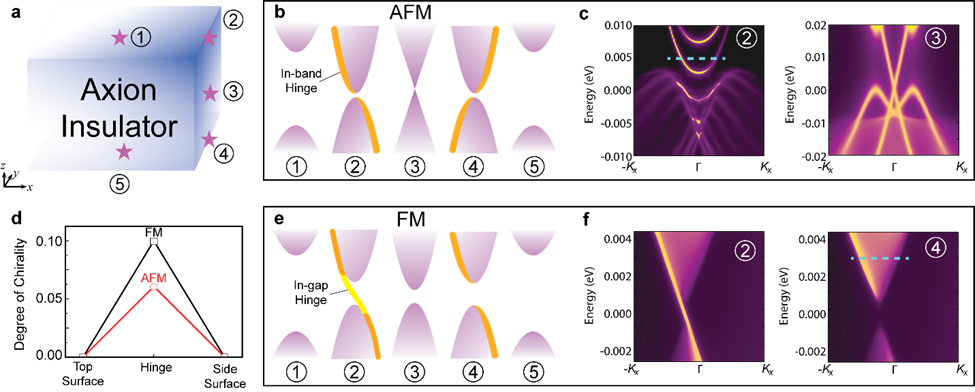
Figure 2 Surface states and hinge states in the ferromagnetic and antiferromagnetic axion insulators.

It is clear that there is a difference between the edge states in the ferromagnetic and antiferromagnetic states. In the ferromagnetic phase, there is an in-gap hinge state crossing the Fermi surface at the edge. On the other hand, the antiferromagnetic axion insulator does not have edge states within the band gap. Instead, both of them have a chiral valence band and conduction band, the so-called in-band hinge state, a representation of the topological nature of the electronic band structure.  This study provides guidance for the realization of the future experimental setup.

Mingqiang Gu, Research Associate Professor of Qihang Liu’s research group, and Jiayu Li, a 2020 doctoral student, are the co-first authors of this article. Qihang Liu, Assistant Professor of the Department of Physics at SUSTech, and Jianpeng Liu, Associate Professor of Shanghai University of Science and Technology, are the co-corresponding authors. In addition, collaborative efforts from Assistant Professor Chang Liu and Professor Haizhou Lu are acknowledged. This research has been supported by the National Natural Science Foundation of China (NSFC), the Key R&D Program of the Ministry of Science and Technology (MOST).

Paper link: https://www.nature.com/articles/s41467-021-23844-z