Recently, a research group from the Shenzhen Institute for Quantum Science and Engineering (SIQSE) and the Department of Physics at the Southern University of Science and Technology (SUSTech) has made progress in the stability of 3D higher-order topological insulators against Coulomb’s interaction. Their work, entitled “Coulomb Instabilities of a Three-Dimensional Higher-Order Topological Insulator,” was published in Physical Review Letters.
In 2005, Kane and Mele theoretically proposed a scheme to realize the quantum spin Hall effect in graphene. The beautiful but straightforward model inspired many condensed-matter physicists to study the topological phases. In the following fifteen years, many extravagant topological phases were proposed by theory or found by experiments, such as the three-dimensional topological insulators, the Weyl semimetal, the quantum, and anomalous Hall effects. Kane and Mele received several prizes due to their model. The Nobel prize in physics was awarded to Thouless, Haldane, and Kosterlitz for theoretical discoveries of topological phase transitions and topological phases of matter.
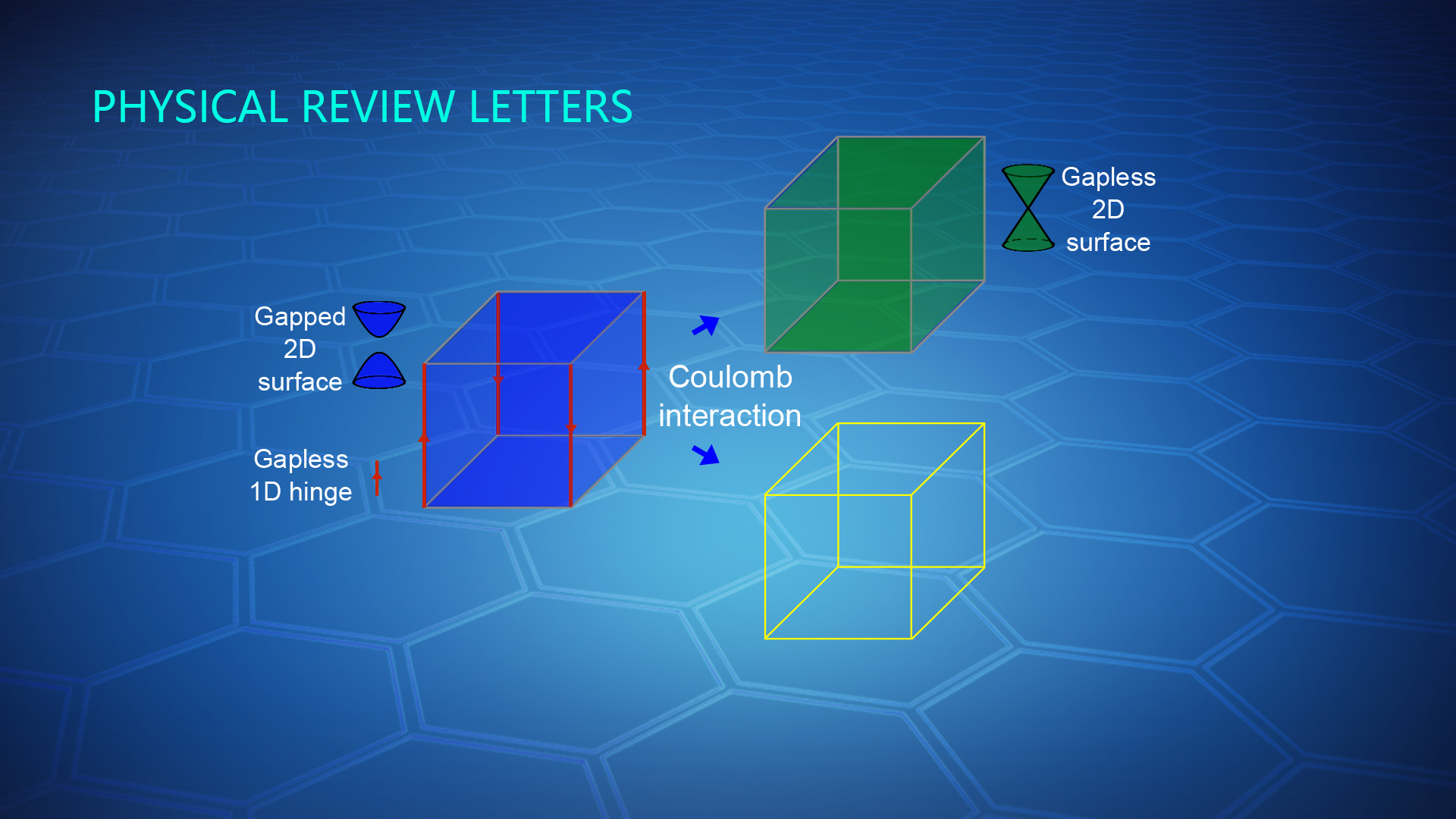
In 2017, Bernevig and his collaborator published a paper in Science, in which they extended the concept of topology from first order to higher order. Compared with conventional topological phases, one of the simplest 3D second-order topological insulators hosts 3D gapped bulk states in its interior but topologically protected gapless 1D hinge states and gapped 2D surface states on its surfaces (Fig.1).
Although the picture for higher-order topology is interesting, there are few observations of higher-order TIs in electronic systems. Instead, there has been experimental evidence for the higher-order topology in bosonic systems. Such higher-order topology is very hard to observe in electronic systems and raises concerns about the stability of higher-order TIs against, e.g., disorder and electron-electron interactions.
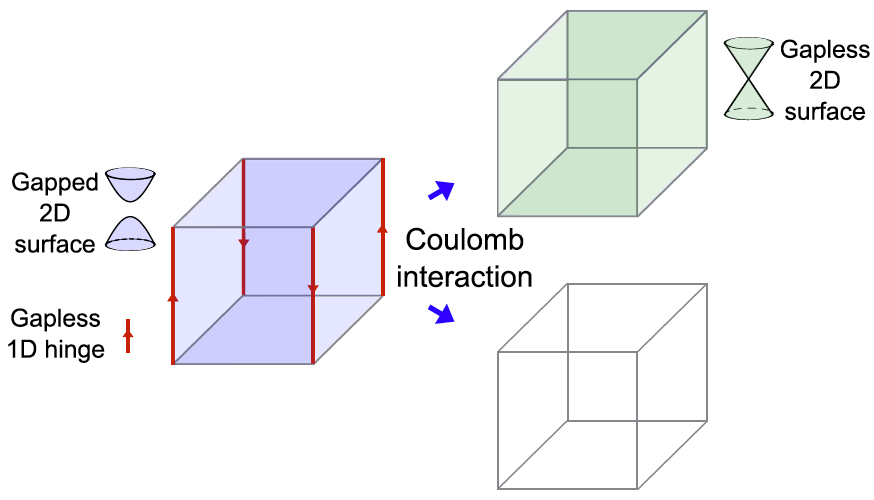
Figure 1. Schematic of a typical 3D second-order TI (left) that hosts 3D gapped bulk states in the interior but topologically protected 2D massive (gapped) Dirac cones on the surfaces and gapless 1D chiral hinge states. It may turn to a TI (right-top) or a NI (right-bottom) in the presence of the Coulomb interactions.
To investigate whether the higher-order topology is stable against the Coulomb interaction between electrons, the theory proposed by Prof. Hai-Zhou Lu’s group, also from SUSTech, first answers this question. They introduced the Coulomb interaction to a widely accepted model of a 3D higher-order topological insulator.
After complete renormalization-group calculation, they obtained the band parameters’ interaction-induced renormalization, which determines the topological invariant. By analyzing the low energy behaviors of the renormalized parameters, they found that the higher-order TIs are always unstable. Two types of topological phase transitions could happen (Fig. 1).
In the first type, a topological phase transition from a second-order TI to TI happens in the presence of the Coulomb interaction. This transition is accompanied by the surface gaps close in the low-energy limit and emergent time-reversal and inversion symmetries. In the second type, the Coulomb interaction could induce another topological phase transition from a second-order TI to a normal insulator (NI), accompanied by the bulk gap close and reopen and appearance of novel quantum criticality. They obtained several phase diagrams in the plane of Coulomb interaction and other parameters (Fig. 2).
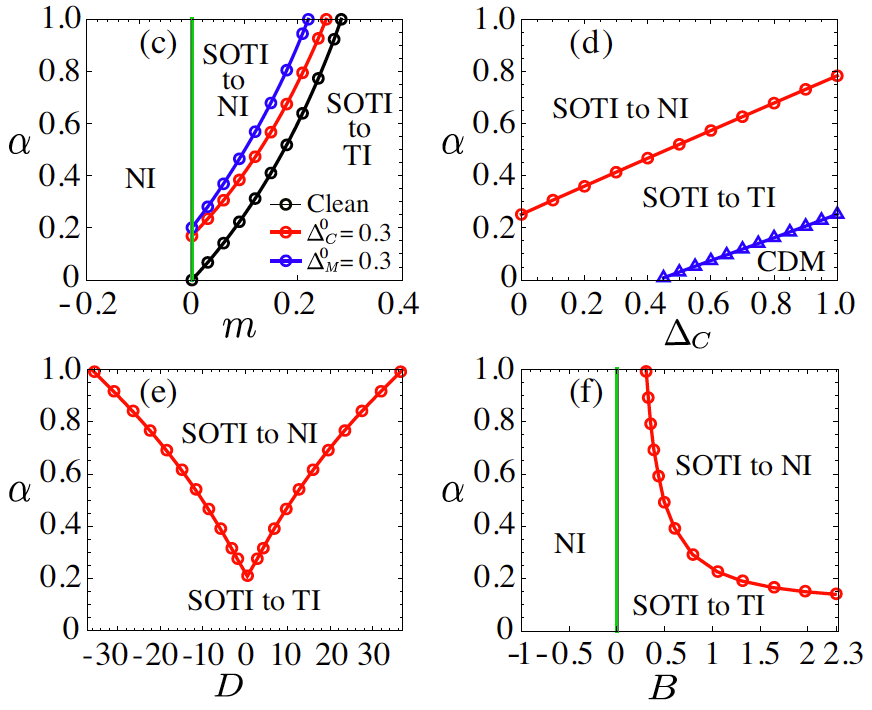
Figure 2. Phase diagrams (c)-(f) in the m–α, ΔC–α, D–α, and B–α planes, respectively. SOTI and CDM stand for the second-order topological insulator and compressible diffusive metal, respectively.
Their theory studies the stability of higher-order topology against electron-electron interactions. With higher-order topological phases predicted, this theory will inspire more exciting research in theory and experiment.
The first author of the work is Dr. Peng-Lu Zhao, and the corresponding author is Prof. Hai-Zhou Lu. The co-authors include Xiaobin Qiang from SUSTech and Academician X. C. Xie from Peking University.
This work was supported by the National Natural Science Foundation of China (NSFC), the National Basic Research Program of China, the Strategic Priority Research Program of Chinese Academy of Sciences (Guangdong Province), Shenzhen High-Level Special Fund, and the Science, Technology and Innovation Commission of Shenzhen Municipality.
The Center for Computational Science and Engineering at SUSTech assisted with the numerical calculations for this study.
Paper link: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.176601
Proofread ByAdrian Cremin, Yingying XIA
Photo By