Landauer’s principle is a physical principle pertaining to the lower theoretical limit of energy consumption of computation, which implies a limit on the information throughput of irreversible computers as real hardware has finite power dissipation tolerance.

The energy cost of binary transistor switching is extrapolated to reach the Landauer limit around 2035. This cost leads to a crucial concern that digital information processors are expected to consume one-fifth of the world’s electricity in the next ten years. Moreover, the energy expended is dissipated as heat into the computer, and computers are already speed-constrained by power dissipation tolerance limits.

This leads to the question of how far it is possible to lower this inescapable energy cost of irreversible computing: the energy cost of resetting bits. This is related to the role of information in thermodynamics.

A group of researchers has derived a universal lower bound for the finite-time work penalty in bit reset, an elementary operation in irreversible computation. The bound applies to all physical models as long as the detailed balance is respected and, thus, encompasses previous results focused on specific models.

Their collaborated work, entitled “Universal bound on energy cost of bit reset in finite time,” was published in the high-impact academic journal Physical Review Letters. This achievement was contributed by researchers from the Southern University of Science and Technology (SUSTech) and scholars based in Germany and Australia.

Landauer’s principle states that bit reset must cost at least k_BTln2 amount of energy, where k_B is Boltzmann’s constant and T the temperature of the ambient environment, i.e., the computer.

To achieve the k_BTln2 limit, quasistatic protocols are required and often assumed possible. However, real-life bit reset takes place at a specific time. This necessitates a possibly dramatically higher work cost than k_BTln2: there is a finite-time work penalty to bit reset. Understanding this penalty is crucial to the energy efficiency of computers in the approaching Landauer’s limit of irreversible computing.

For this model, substantial results recently show that the work penalty of an optimal reset protocol scales as 1/τ for scenarios such as vanishing reset error or local equilibrium. Meanwhile, a theoretical model based on a qubit reset indicates a more benign scaling. The tension between these results and the multitude of possible hardware implementations of bits, including colloidal systems and fluctuating RC circuits, motivates a search for a universal Landauer’s principle that holds in finite time regardless of the physical implementation and guides novel hardware beyond CMOS technology.

In this study, Dr. Yi-Zheng Zhen and Associate Professor Oscar Dahlsten from the Department of Physics and the Shenzhen Institute for Quantum Science and Engineering (SIQSE) at SUSTech analytically derived a universal lower bound for the finite-time work penalty in bit reset. The bound applies to all physical models as long as the detailed balance is respected and encompasses previous results focused on specific models such as those depicted in Fig.1(a) and (b).

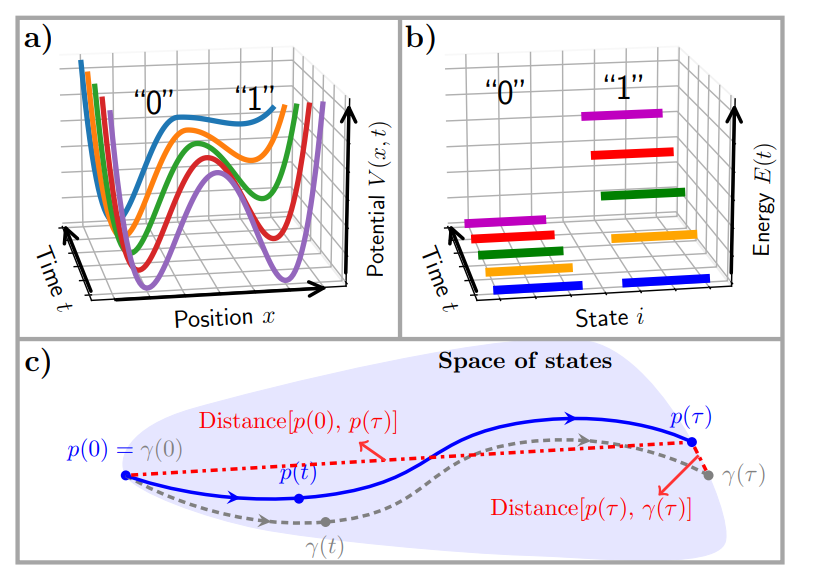
Figure 1: Analysis of a wide range of bit-reset scenarios. a) a double-well potential V (x, t), which is gradually turned into a single well, b) a system with two energy levels where one level is lifted gradually. c) During the finite-time bit-reset, the system state p(t) lags behind the thermal state γ(t) and shows two distances are closely related to the minimal work cost.

The bound also holds for both the total time region and the finite bit reset error and can be viewed as a refined Landauer’s principle for finite and infinite time. The proof of the bound implies that the work penalty is optimized if one adopts a truly two-level system, such as a spin.

The researchers further applied the bound to induce an upper limit on the information throughput of irreversible computers. These results would aid nano-electronics research on alternative hardware and extend information thermodynamics to finite time non-equilibrium regimes.

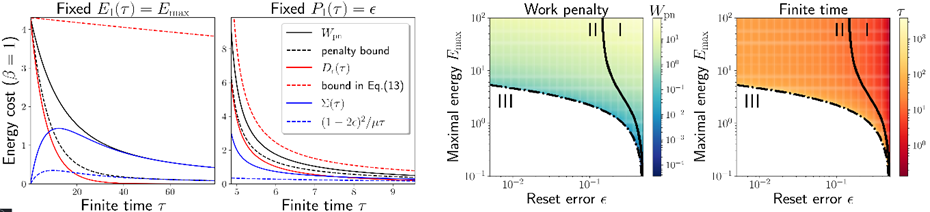
Figure 2: Researchers show how the additional work cost changes with the finite-time and reset error.

Dr. Yi-Zheng Zhen from the Hefei National Laboratory for Physical Sciences at the Microscale (HFNL) at the University of Science and Technology of China (USTC) is the first author of this paper. He was a postdoctoral fellow at SUSTech’s SIQSE for much of this work.

The co-authors are Dr. Dario Egloff of the Technical University of Dresden and the Max-Planck Institute for the Physics of Complex Systems in Dresden, and Prof. Kavan Modi of Monash University in Melbourne. Assoc. Prof. Oscar Dahlsten of SUSTech is the corresponding author.

This work was supported by the National Science Foundation of China (NSFC), the Swiss National Science Foundation (SNSF), and the Australian Academy of Technology and Engineering (ATSE).

Paper link:  https://link.aps.org/doi/10.1103/PhysRevLett.127.190602

To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.