Professor Stavros Garoufalidis from the International Center for Mathematics of the College of Science at the Southern University of Science and Technology (SUSTech) has recently collaborated with Professor Nathan M. Dunfield from the Department of Mathematics at the University of Illinois and Professor J. Hyam Rubinstein from the School of Mathematics and Statistics at the University of Melbourne.
Their research, entitled “Counting essential surfaces in 3-manifolds”, was published in the high-impact journal Inventiones Mathematicae, regarded as one of the most prestigious mathematics journals in the world.

The researchers consider the natural problem of counting isotopy classes of essential surfaces in 3-manifolds, focusing on closed essential surfaces in a broad class of hyperbolic 3-manifolds. Their main focus is that the count of (possibly disconnected) essential surfaces in terms of their Euler characteristic always has a short generating function and hence has quasi-polynomial behavior.
This gives remarkably concise formulae for the number of such surfaces, as well as detailed asymptotics. They give algorithms that allow computing these generating functions and the underlying surfaces and apply them to almost 60,000 manifolds, providing a wealth of data about them. The researchers used this data to explore the delicate question of counting only connected essential surfaces and propose some conjectures.
The methods by Prof. Garoufalidis and his collaborators involve normal and almost normal surfaces, especially the work of Tollefson and Oertel, combined with techniques pioneered by Ehrhart for counting lattice points in polyhedra with rational vertices. They also introduced a new way of testing if a normal surface in an ideal triangulation is essential that avoids cutting the manifold open along the surface. Instead, they used almost normal surfaces in the original triangulation.
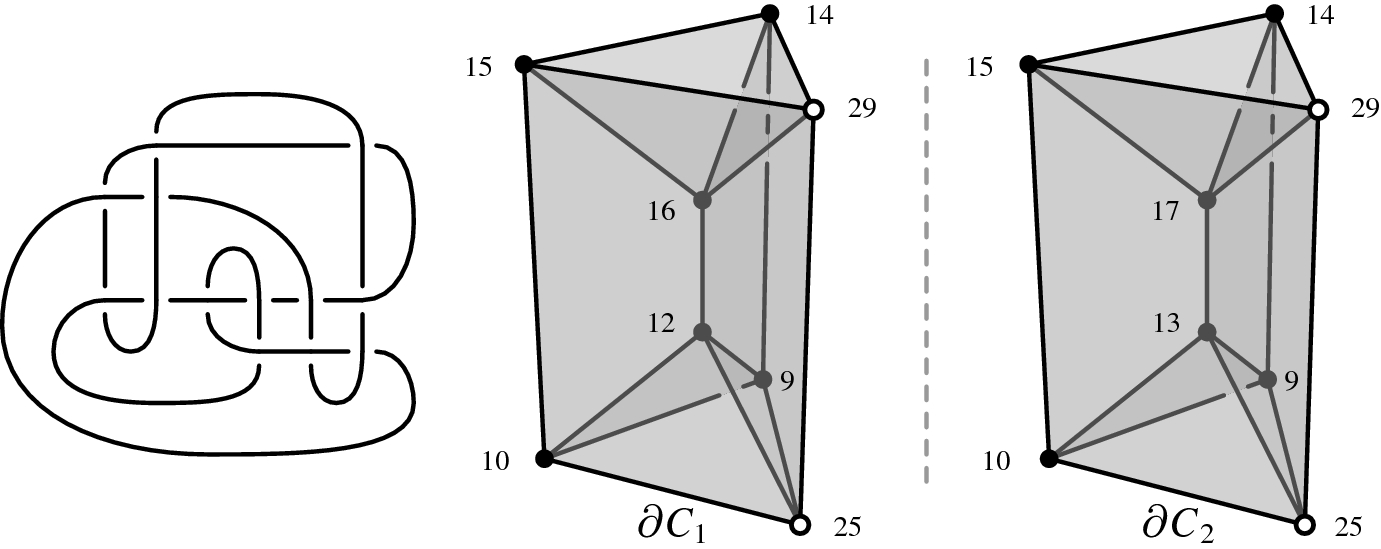
Figure 1. The knot K 13n1019. For a 15-tetrahedra triangulation of the exterior of the knot K 13n1019 (left), the complex that computes the incompressible surfaces (right) consists of two 4-dimensional faces with the same combinatorics that are glued together along a single 3-dimensional face.
It was found that the counting of incompressible surfaces by Euler characteristics in 3-manifolds is an interesting (quasi)-polynomial. Using the SnapPea database of 3-manifolds and a considerable amount of coding revealed the structure of such counting for thousands of examples. An additional counting of incompressible surfaces by their numbers of holes (genus) was given, and this leads to irregular counting of arithmetic nature, with patterns similar to those of prime numbers. For instance, the counting of such surfaces by genus on the 3-dimensional manifold o9_42517 (made out of 9 tetrahedra), leads to the sequence of numbers 6, 4, 10, 14, 26, 26, 52, 46, 76, 76, 118, 96, 172, 136, 194, 196, 286,212, 354, 274, 388, 360, 506, 378, 604, 490, 634, 574, 820, 568, 948,728, 946, 846, 1122, 864, 1356, 1040, 1316, 1146, 1644, 1140, 1800,1392, 1716, 1570, 2136, 1506, 2332, 1752 whose general formula and pattern is not known.
Prof. Stavros Garoufalidis from SUSTech, Prof. Nathan M. Dunfield from the University of Illinois, and Prof. J. Hyam Rubinstein from the University of Melbourne are the co-first and corresponding authors of this paper.
This work was supported by the International Center for Mathematics at SUSTech, the Department of Mathematics at the University of Illinois, and the School of Mathematics and Statistics at the University of Melbourne.
To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.
Proofread ByAdrian Cremin, Yingying XIA
Photo By