The concepts of topology and symmetry have revolutionized many branches of physics, ranging from condensed matter physics to cold atoms, photonics, acoustics, and mechanics, as manifested by the classification of topological phases of matter. A fundamental dichotomy for topological classification is whether the studied systems are spinful or spinless. Remarkably, these two spin classes can exhibit distinct topological phases under internal or space group symmetries. For instance, under PT symmetry, the spinful class has Kramers’s degenerate bands, while the spinless class has real non-degenerate bands; these band structure differences enable unique topological phases in each class. Therefore, the spin class seems to impose a fundamental limitation on the possible topological phases that a system can realize.

Recent theoretical breakthrough [Phys. Rev. Lett. 126, 196402 (2021)] has revealed a remarkable possibility to break this fundamental limitation by exploring the previously overlooked gauge symmetry to projectively represent and completely change the fundamental symmetry algebra of the original system. Thus, it can switch the spinless to spinful topological phases, or vice versa, with projective PT symmetry. However, switching between spinless and spinful topological phases, namely, making an original spinless (spinful) system behave as a spinful (spinless) one, has never been experimentally realized in any physical system.

Associate Professor Zhen Gao’s group from the Department of Electronic and Electrical Engineering at the Southern University of Science and Technology (SUSTech) has recently reported unambiguous experimental evidence of the spinful topological phases in “spinless” acoustic crystals, which overcomes the fundamental limitation on topological phases by spin classes.

Their paper, entitled “Spinful Topological Phases in Acoustic Crystals with Projective PT Symmetry,” has been published in Physical Review Letters, one of the most prestigious journals in physics.

Prof. Gao’s group started by designing 1D topological acoustic crystals that were fabricated by using a standard 3D printing technique. By introducing negative and positive coupling coefficients to engineer an effective Z₂ gauge field in acoustic crystals, the projective PT symmetry can completely modify the fundamental symmetry algebra of a system, making an originally spinless system behave like a spinful one.

They then observed the Kramers double-degenerate band structures and the Kramers pairs of topological boundary modes in acoustic crystals, which were previously unique to spinful systems. The double-degenerate topological states can not only act as ideal carriers of acoustic information transport with multiple transmission channels, but also can increase the density of states which may have promising potential applications in phononic lasing and sound power emission.

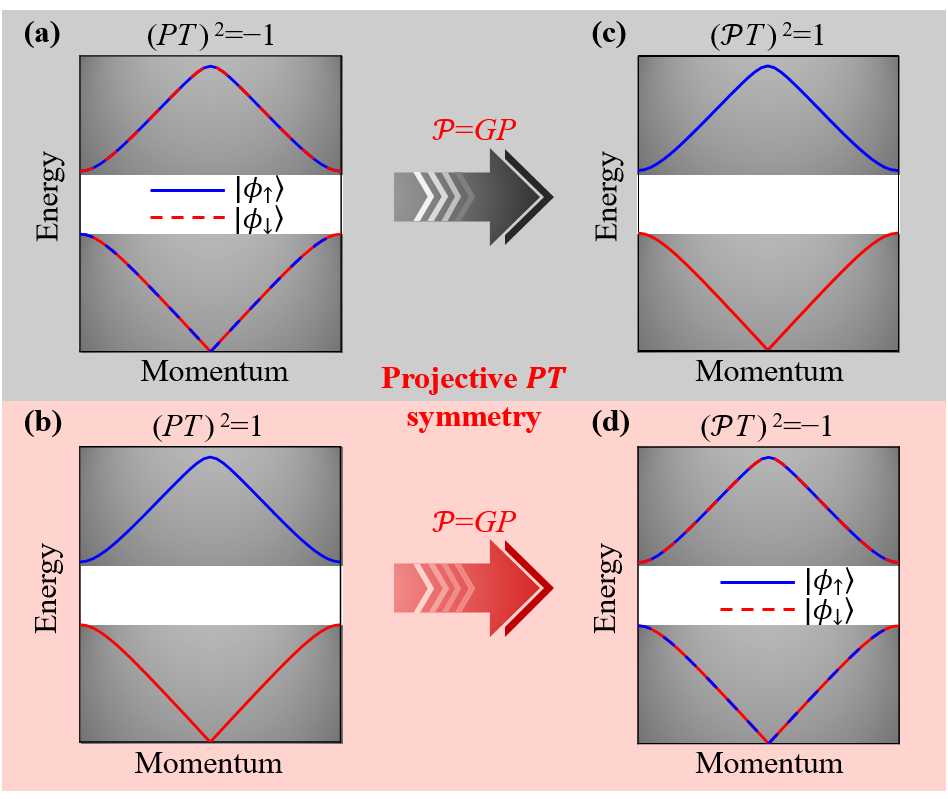
Figure 1. Switching spinless and spinful topological phases with projective PT symmetry

Figure 1 shows a schematic diagram of the switching between spinless and spinful topological phases with projective PT symmetry. The combination of space inversion symmetry (P) and time-reversal symmetry (T) is spacetime inversion symmetry (PT), which can act as a criterion to classify the spinless or spinful phases of a system. The spinful class satisfies (PT)² = -1, enforcing double-degenerate bands in the entire Brillouin zone (BZ) [Figure 1(a)]. By contrast, the spinless class satisfies (PT)² = 1, dictating real non-degenerate band structures [Figure 1(b)]. However, in the presence of gauge symmetry, the space inversion symmetry P will be projectively represented as P’= GP, where G is a gauge transformation. Properly choosing G, the projective PT symmetry (i.e., P’T) can satisfy (P’T)² = 1 for spinful systems [Figure 1(c)], or satisfy (P’T)² = -1 for spinless systems [Figure 1(d)]. This surprisingly suggests that the projective PT symmetry can exchange the fundamental symmetry algebra of spinless and spinful systems, enabling the switching between spinless and spinful topological phases.

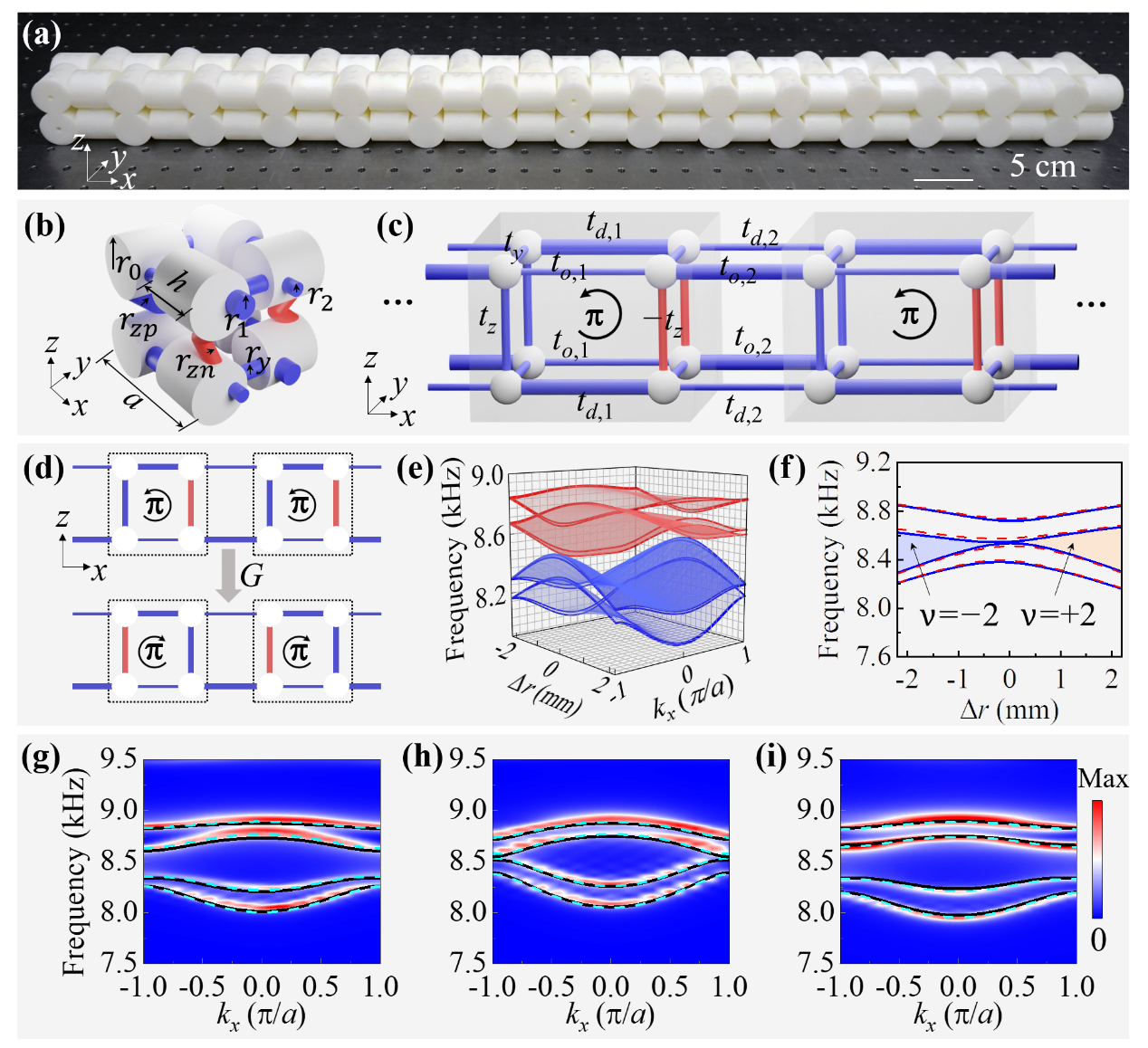
Figure 2. Experimental demonstration of Kramers double-degenerate band structures

Figure 2(a) shows the designed 1D acoustic crystal, which is fabricated with a standard three-dimensional (3D) stereolithography technique. A unit cell of the acoustic crystal is shown in Figure 2(b), the coupling tubes with positive and negative coupling coefficients are indicated by blue and red colors, respectively. Through the introduction of positive and negative coupling, Prof. Gao’s group designed an effective Z₂ gauge field in the acoustic crystal, and then realized the projective representation of the space inversion symmetry. Figures 2(c) and (d) are the configuration diagram of the tight-binding model and the diagram of the gauge transformation process, respectively.

It can be seen that the gauge transformation only changes the sign of the coupling coefficient in the z- direction, and the coupling in other directions remains unchanged. Figures 2(e) and (f) are the simulated band structure phase diagram of the acoustic topological insulator and the evolution diagram of its band gap with geometric parameter Δr, respectively. Figures 2(g) to (i) show the simulated (line diagram) and measured (color diagram) band structures of the acoustic crystals with different Δr, respectively. The band gaps evolve from opening to closing and then reopening, and the winding number for the acoustic crystal evolves from v = -2 to v = 2. The simulated and experimentally measured results directly prove that the acoustic crystal always satisfies (P’T)² = -1 during the evolution of Δr as it always possesses a double degenerate band structure in the entire Brillouin zone.

Figure 3. Observation of Kramers pairs of topological boundary modes

Based on the first-principles calculation, the acoustic crystals with Δr exhibit nontrivial spinful topological phases with nonzero 2Z winding numbers. Kramers pairs of topological boundary modes are guaranteed by the bulk-edge correspondence. Figure 3 (a) shows the numerically calculated eigenfrequency spectrum of a finite 1D acoustic crystal (15 unit cells) with Δr=2.2 mm. Two pairs of topological boundary modes (colored dots) localized at the left or right ends can be observed within the bandgap of bulk states (grey squares). The measured intensity spectra are shown in Figure 3(c); within the bulk bandgap regime (about 8.3 to 8.5 kHz), the intensity spectrum of the edge region remains much higher than that of the bulk region, indicating the existence of edge states.

Figures 3(b) and (d) show the simulated acoustic pressure distributions of the four topological boundary states and the experimental measurement results from the full-field scanning, respectively. The acoustic pressure distribution is only localized at the boundary of the sample, which intuitively implies the localization feature of the topological boundary states. At the same time, the experimental results also show that when excited by acoustic point sources (indicated by red or blue stars) with designed phases difference (0 or π), the measured phase distribution of the boundary states has the same phase difference. Hence, the four topological boundary states are all orthogonal. The measured acoustic pressure distributions of the Kramers pairs of topological boundary modes localized on the left or right edges of the 1D acoustic crystal, matching well with the simulated results shown in Figure 3(b).

Figure 4. Topological interface states between two spinful topological acoustic crystals with opposite topological invariants

Figure 4(a) shows the fabricated sample, which consists of 8 unit cells with winding number v = -2 on the left side and 8 unit cells with winding number v = +2 on the right side, and the red plane indicates the interface. According to the bulk-edge correspondence, the total number of topological interface states should be exactly equal to the difference between the winding numbers of two nontrivial topological acoustic crystals (i.e., 4). Figure 4(b) shows the simulated eigenfrequency spectrum of the acoustic crystal, and four topological boundary states (colored stars) can be seen within the bulk band (gray square). More intuitively, Figure 4(c) shows the measured average intensity of the interface state (red) and bulk (grey) regions in the frequency regime of 7.4 to 9.2 kHz. In the 8.3 to 8.5 kHz frequency regime, the intensity peak of the interface region is located within the bulk bandgap, implying the existence of topological interface states. Furthermore, through simulated calculation and full-field scanning measurement, Figures 4(d) and (e) respectively show the acoustic filed distributions of the topological interface states.

Both the experimental and theoretical results show that the acoustic pressure distributions of the topological interface states are localized in the vicinity of the interface and decay exponentially away from it. The interface states observed from simulations and experimental measurements directly prove that four topological interface states exist in the one-dimensional acoustic topological insulator shown in Figure 4(a).

Yan Meng, Research Asst. Prof. from the Department of Electronic and Electrical Engineering at SUSTech, Shuxin Lin, an undergraduate student from the Department of Physics at SUSTech (now a Ph.D. candidate at Nanyang Technological University), and Binjie Shi, a master’s student from Jiangsu University, are the co-first authors of this paper. Assoc. Prof. Zhen Gao from SUSTech, Prof. Yihao Yang from Zhejiang University, and Prof. Hongxiang Sun from Jiangsu University are the co-corresponding authors. SUSTech is the first affiliation.

This research was supported by the National Natural Science Foundation of China (NSFC), Fundamental Research Funds for the Central Universities, Excellent Young Scientists Fund Program (Overseas) of China, National Key Research and Development Program of China, and SUSTech.

Paper link: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.130.026101

To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.