Symmetry represents the property of a system or physical law remaining unchanged under specific transformations, constituting a fundamental concept in modern physics. However, in reality, most symmetries are broken; for instance, the left and right halves of the human body do not strictly adhere to mirror symmetry but only approximately satisfy it. Understanding the effects of these approximate symmetries on physical systems remains an intriguing yet unresolved challenge.

The research group led by Professor Qihang Liu from the Department of Physics at the Southern University of Science and Technology (SUSTech) has recently made progress in the group theory of quasisymmetry in condensed matter systems and the protected near degenerate band structures.

Their research results, entitled “Group Theory on Quasisymmetry and Protected Near Degeneracy”, have been published in the journal Physical Review Letters.

Group theory is a mathematical tool for studying symmetry, which always leads us to universal conclusions. It holds strong capabilities in predicting whether symmetry-related effects are present or not. For instance, by group theory, we know whether the energy bands will cross or anti-cross, or whether the excitation from one quantum states to other will happen. However, when the symmetries are broken, group theory is ineffective in characterizing approximately held symmetries.

In the field of band structures, high degeneracies of energy bands are insured by high symmetries (see Fig. 1a). While conventional group theory could answer whether the degenerate bands will be split after introducing symmetry-lowering terms, it could not address the magnitude of the splitting, which is closely related to approximate symmetry. Therefore, there is a need to generalize the present group-theoretical framework in condensed matter systems for further exploring the approximate symmetry.

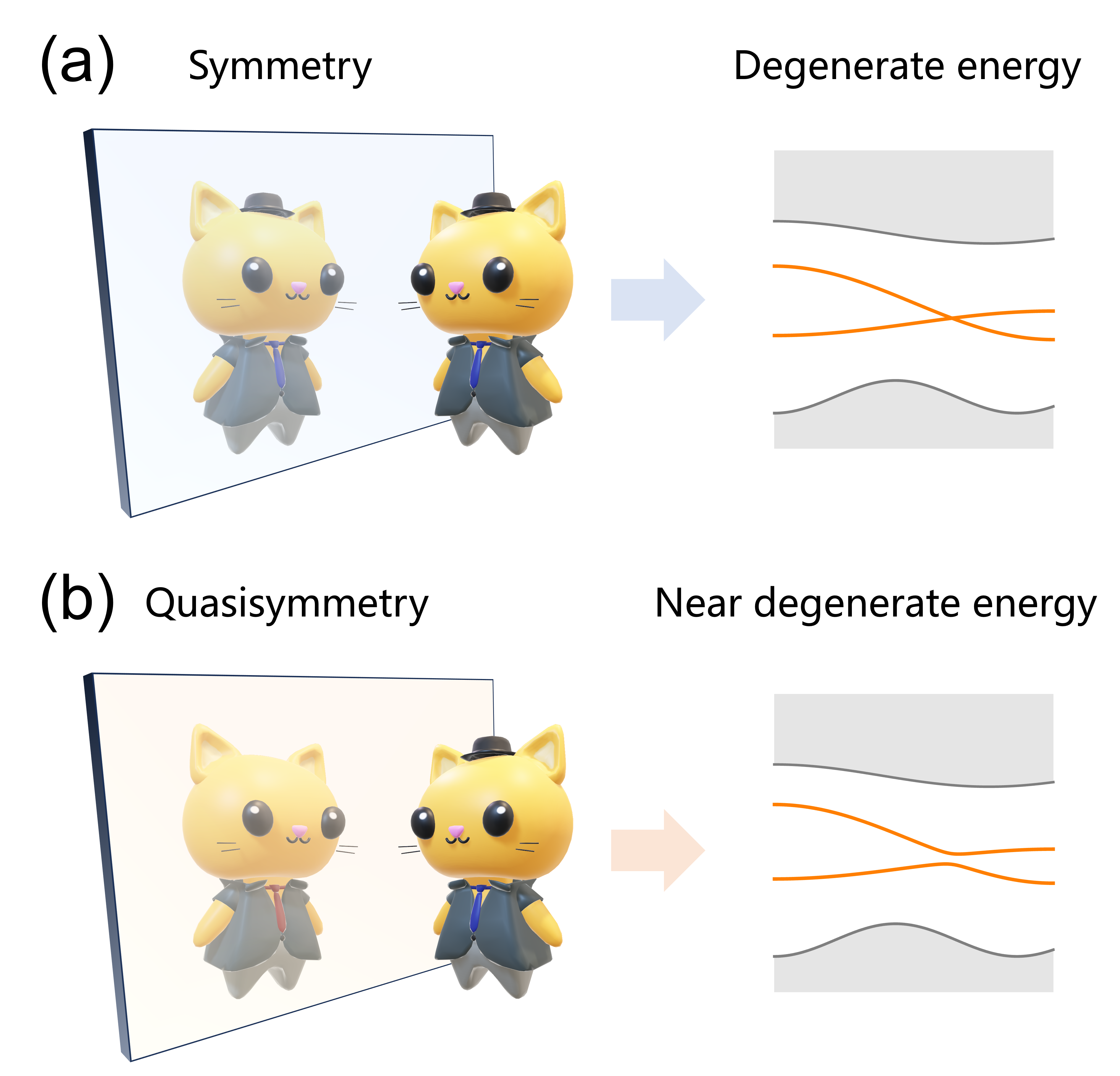
Figure 1. Sketches of symmetry and quasisymmetry. (a) Symmetry protects degeneracy in energy bands. (b) Quasisymmetry protects near degeneracy in energy bands.

Historically, researchers in distinct fields gradually realized that the presence of approximate symmetry has nontrivial influences, bringing us a variety of related concepts such as pseudo-symmetry (Pieter de Wolff, 1967), fuzzy symmetry (Paul Mezey, Jean Maruani, 1990), and quasisymmetry (Philip Moll, Andrei Bernevig, Chao-Xing Liu, 2022). Focusing on crystalline systems, the research group was interested in building a connection between quasisymmetry and near degenerate bands. They aimed to establish a universal group theory to potentially offer a new and efficient way for diagnosing and designing materials with significant Berry curvature and colossal anomalous transport effects.  

In this study, the researchers developed the group theory on quasisymmetry within the general perturbation theory and projection procedure. It was found that the subspaces of a Hamiltonian may present hidden symmetries that are not satisfied by the Hamiltonian. Among them, quasisymmetries are those hidden symmetries that forbid the first-order perturbation of a symmetry-lowering term. Moreover, as the quasisymmetries are broken by the second-order perturbation, the energy splitting of degenerate bands are ensured to be small under the protection of quasisymmetries (Fig. 1b). By applying the representation theory on the newly defined quasisymmetry group, they derived the necessary conditions for the existence of quasi-symmetry in realistic materials, covering the possible quasisymmetries in crystallographic point groups and Lie groups.

Based on this new group theory, the group predicted the topological phase transition in Dirac nodal line semimetal AgLa. The Dirac nodal line is fully gaped by spin-orbit coupling but exhibits two tiny-gapped Dirac cones with a 6 meV gap protected by inversion symmetry as quasisymmetry. The development of this new group theory reveals the subtle relations between approximate symmetries and band structures, paving a new avenue for designing functional materials with significant Berry curvature-related properties.

Jiayu Li, a Ph.D. student in Professor Qihang Liu’s group, is the first author of the paper. Ao Zhang, a postdoctoral fellow, and Yuntian Liu, a Ph.D. student, are the co-authors. Professor Qihang Liu is the corresponding author, and the Department of Physics at SUSTech is the first affiliated unit of the paper.

This work was supported by the National Key R&D Program of China, National Natural Science Foundation of China (NSFC), Key-Area Research and Development Program of Guangdong Province, Guangdong Provincial Key Laboratory, Guangdong Innovative and Entrepreneurial Research Team Program, and the Shenzhen Science and Technology Program.

Paper link: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.026402

To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.