Higher-order topological insulators (HOTIs) have attracted significant attention due to their ability to support low-dimensional boundary states. For instance, two-dimensional (2D) HOTIs can exhibit one-dimensional (1D) edge states and zero-dimensional (0D) corner states. However, compared to their 2D counterparts, three-dimensional (3D) higher-order topological phases hold even greater promise—theoretically supporting first-order 2D surface states, second-order 1D hinge states, and third-order 0D corner states. This capability enables multidimensional wave manipulation and could substantially enhance device integration density.

Traditionally, realizing 3D HOTIs requires guidance from tight-binding models with higher-order band topology, which can be directly and conveniently mapped to scalar wave systems such as 3D phononic crystals and electrical circuits. However, due to the vectorial nature of electromagnetic waves and the lack of mirror symmetry perpendicular to the confinement direction, the eigenmodes in 3D photonic crystals cannot be simply classified as transverse electric (TE) or transverse magnetic (TM) scalar modes. This results in complex band dispersion, making it extremely challenging to describe 3D vectorial electromagnetic systems using simple tight-binding models.

Breaking this barrier, Associate Professor Zhen Gao’s research group from the Department of Electronic and Electrical Engineering at the Southern University of Science and Technology (SUSTech) has successfully realized a 3D photonic HOTI within a metal-cage photonic crystal (MCPC) resembling a tight-binding model. This structure simultaneously supports first-order surface states, second-order hinge, and third-order corner states within the same photonic crystal. Notably, all topological states exhibit self-guided wave propagation without requiring additional cladding layers and demonstrate strong robustness. This breakthrough opens new pathways for designing 3D topological photonic devices, with potential applications in high-dimensional light manipulation and robust anti-interference lasers.

Their findings were published in Nature Communications under the title “Realization of a three-dimensional photonic higher-order topological insulator”.

The research team successfully implemented a 3D Su-Schrieffer-Heeger (SSH) model using an MCPC structure (Figure 1b). In this design, each dielectric column is surrounded by four metal columns, creating confined Mie resonance states with slow decay characteristics. This innovative configuration effectively reduces the vectorial electromagnetic waves in the 3D photonic crystal to scalar waves, resulting in a band structure that closely mirrors that of a 3D tight-binding model. As demonstrated in Figures 1e and 1f, the finite structure exhibits third-order band topology, with the 3D photonic crystal supporting topological surface states (first-order), hinge states (second-order), and corner states (third-order). The eigenmode field distributions clearly confirm the coexistence of these distinct topological boundary states within a single platform.

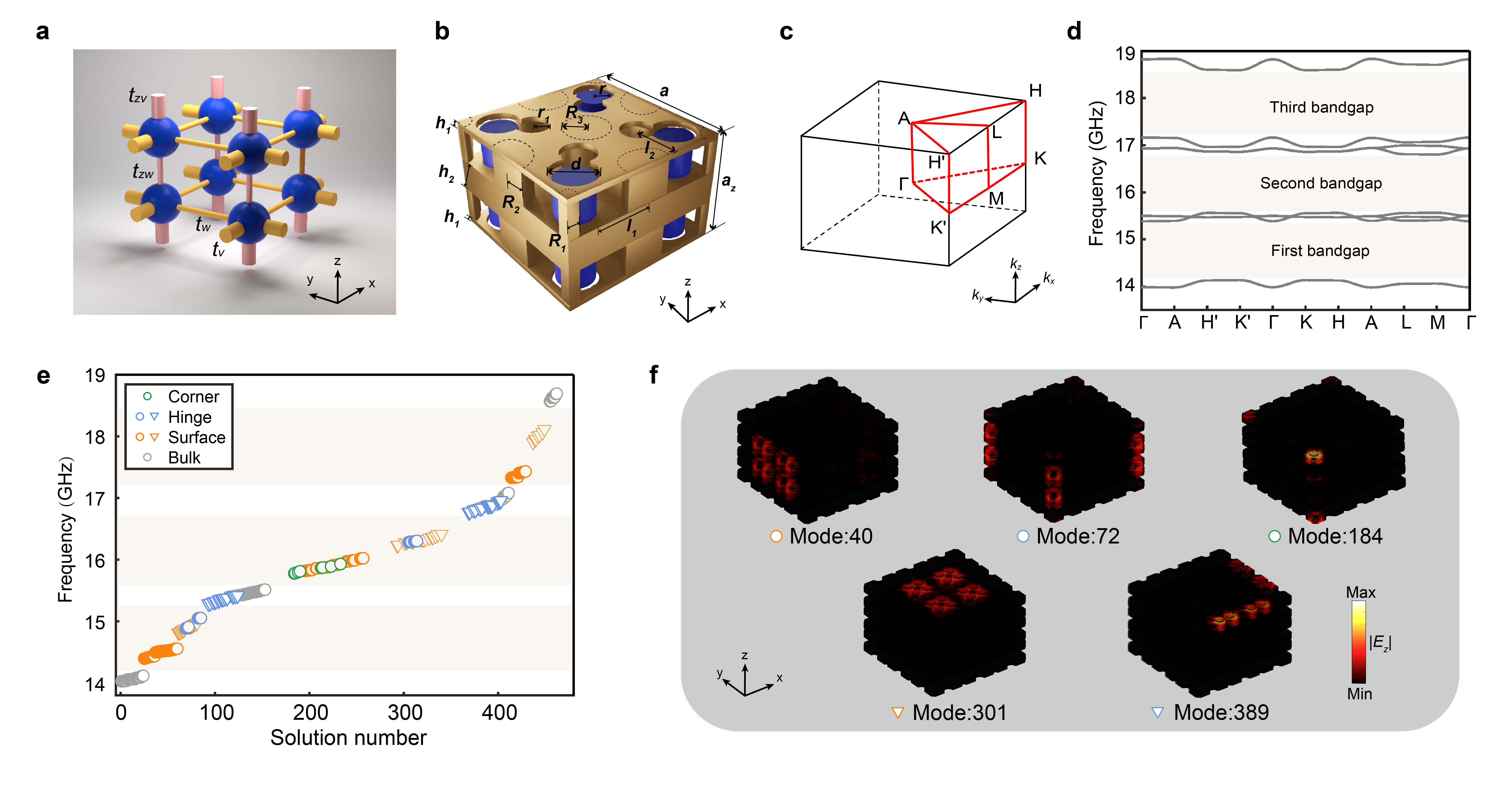
Figure 1. Design of a 3D photonic HOTI. Experimental observation of the first-order photonic topological surface states.

The fabricated experimental sample consists of 20 unit cells along the x and z directions and 4 unit cells in the y direction. Perforated copper plates (golden) and air foams (white) are used to induce vertical interlayer and intralayer couplings while also stabilizing the placement of the metallic and dielectric rods. Calculated topological surface state dispersions (orange lines) along high-symmetry lines of the projected 2D surface Brillouin zone (BZ) show first-order topological surface states within all three photonic bandgaps, completely separated from bulk bands (grey lines). Notably, these surface states exhibit well-defined dispersions even within the light cone continuum, indicating negligible leakage to the surrounding air. This phenomenon arises from strong field localization due to confined Mie resonances, which concentrate electric fields around dielectric rods with minimal surface leakage.

Experiments were conducted to measure transmission spectra of topological surface (orange) and bulk (dark grey) states by placing a source antenna (cyan stars) at the center of the front (010) surface and inserting a probe antenna into the surface or bulk. Three photonic bandgaps (floral white) were observed in the bulk transmission spectrum, with sharp peaks in the surface state transmission spectrum within these bandgaps, confirming the existence of topological surface states on the 3D MCPC surfaces. Electric field distributions of the surface states were measured using a probe antenna, showing localization on the sample surface (Figure 2f), consistent with simulations (Figure 2g). Fourier-transforming the measured electric field distributions yielded surface state dispersions (Figure 2h), demonstrating excellent agreement with simulations (white dashed line).

Figure 2. Observation of the first-order photonic topological surface states. Experimental observation of the second-order photonic topological hinge states.

The researchers experimentally demonstrated second-order photonic topological hinge states arising from the higher-order band topology of the 3D MCPC. Simulations showed eigenmode dispersion relationships (Figure 3a), where surface states, hinge states, bulk states, and the light cone are marked by orange, blue, grey, and cyan lines, respectively. Similar to surface states, the simulated field distribution of the hinge state (Figure 3b) shows strong confinement at the hinge even when its dispersion lies within the light cone.

To excite the topological hinge states, a source antenna (cyan stars) was placed at the center of the hinge. Transmission spectra of the hinge (blue) and surface (orange) states were measured (Figure 3c), revealing two sharp peaks in the hinge spectrum within the surface state bandgaps. The measured electric field distribution of the hinge state at 14.9 GHz (Figure 3d) matches the simulation (Figure 3e), confirming field localization at the hinge. The measured hinge state dispersion (color map) along the kz direction, obtained via Fourier transformation of the complex electric field distribution (Figure 3f), also shows excellent agreement with simulations (white dashed line). These results demonstrate the robust existence of second-order topological hinge states in 3D MCPCs.

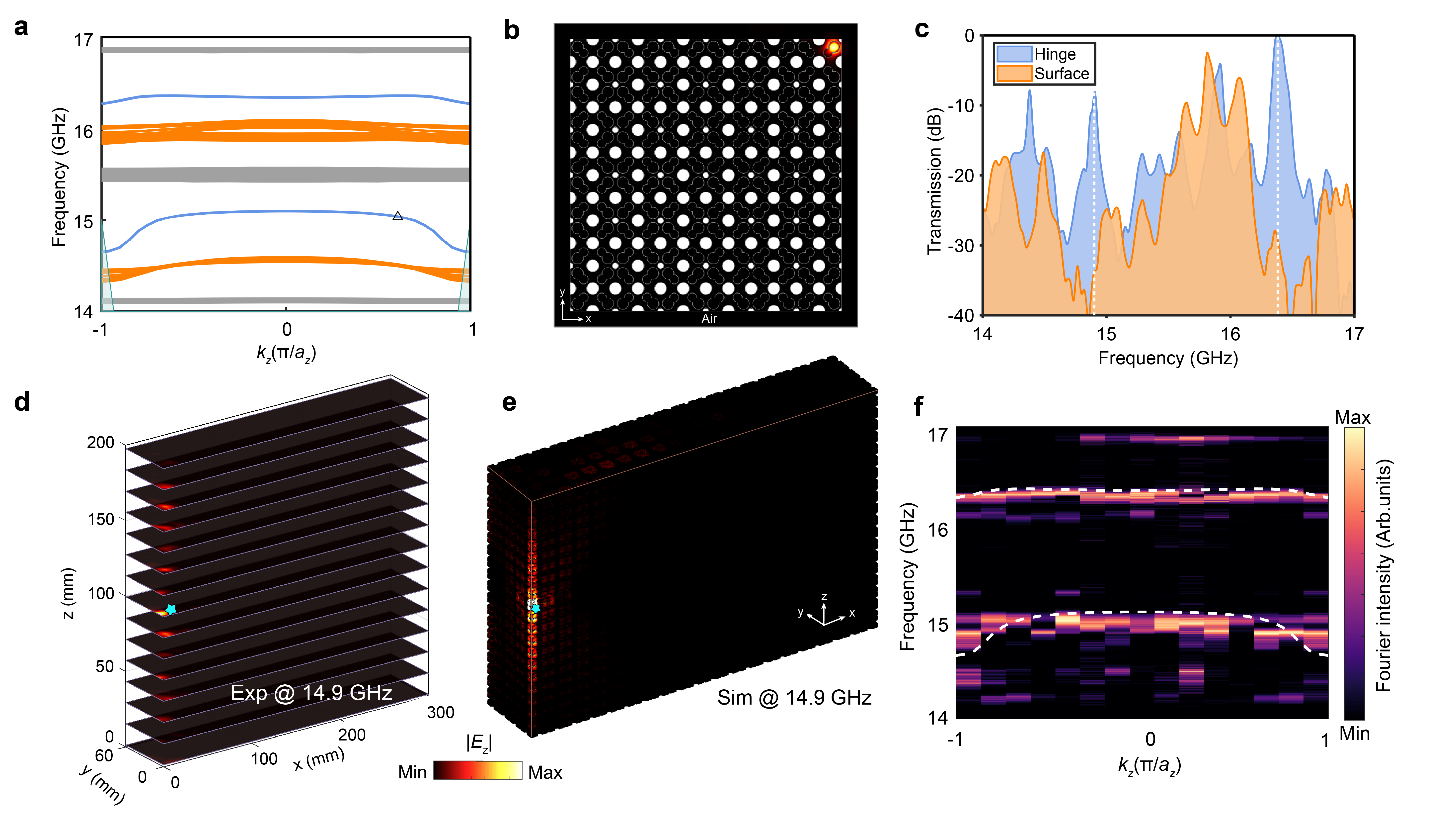
Figure 3. Observation of the second-order photonic topological hinge states. Experimental observation of third-order photonic topological corner states.

They experimentally characterized third-order photonic topological corner states in the 3D MCPC. Transmission spectra of surface (orange), hinge (blue), and corner (green) states were measured using a point source (cyan stars in Figures 4b–4c) placed near the corner. As shown in Figure 4a, the corner measurement exhibited a transmission peak at ~15.8 GHz (white dashed line), consistent with calculated eigenfrequency ranges (Figure 1e). Measured (Figure 4b) and simulated (Figure 4c) electric field distributions at 15.8 GHz show strong localization at the corner, confirming the tightly confined nature of topological corner states.

Figure 4. Observation of the third-order photonic topological corner states. Experimental demonstration of robustness of topological boundary states.

The robustness of these topological surface, hinge, and corner states was demonstrated by introducing defects— specifically, removing dielectric rods at the corresponding boundaries. Insets in Figures 5a–5c (red circles) show experimental measurements, while Figures 5d–5f (white dashed cylinders) show numerical simulations. Measured (Figures 5a–5c) and simulated (Figures 5d–5f) electric field distributions with defects remain nearly identical to those without defects (Figures 2–4), except for reduced fields at defect locations due to missing dielectric rods. These results confirm the robustness of topological boundary states against structural defects.

Figure 5. Experimental demonstration of the robustness of topological surface, hinge, and corner states.

The first author of the paper is master’s student Ziyao Wang at SUSTech. The co-first authors include Associate Researcher Yan Meng at Dongguan University of Technology (DGUT), Lecturer Bei Yan at Wuhan University of Science and Technology, and Ph.D. candidate Dong Zhao at SUSTech. The corresponding authors are Associate Professor Zhen Gao, Assistant Professor Biye Xie at The Chinese University of Hong Kong, Shenzhen, Postdoctoral Researcher Zhenxiao Zhu at SUSTech, and Associate Professor Xiang Xi at DGUT. SUSTech is the first affiliated institution of the paper.

Paper link: https://www.nature.com/articles/s41467-025-58051-7

To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.