Compressibility has a stabilising effect on a variety of high-speed shear flows, including homogeneously sheared turbulence, turbulent mixing layers, and wall-bounded turbulence. The planar mixing shear layer is the simplest flow configuration of practical turbulent flow, devoid of the complexities of wall effect. However, it plays a key role in many applications, including scramjet engines, reduction of supersonic jet noise and inertial-confinement fusion

Numerous studies have attempted to explain the suppression mechanism of compressibility from the perspective of kinetic energy transfer and describing the compressibility effect on coherent structures in mixing layers. But most of the previous studies have focused on the small-scale vortical structures and spanwise Kelvin–Helmholtz vortices in mixing layers.

The physical mechanism of the suppression of layer growth rate due to compressibility is the key scientific problem in mixing layer research. As a result, further analysis is required to better explore the compressibility effects on temporally evolving turbulent mixing layers at various Mach numbers.

Associate Professor Jianchun Wang’s team from the Department of Mechanics and Aerospace Engineering at the Southern University of Science and Technology (SUSTech) has recently made important progress in the study of the suppression mechanism and coherent structures of compressible turbulent mixing layers.

Their paper, entitled “Compressibility effects on statistics and coherent structures of compressible turbulent mixing layers,” was published in the Journal of Fluid Mechanics. The study carries out the DNS of a temporal compressible shear layer to investigate the compressibility effects on statistical properties and coherent structures.

By applying dual-shear layer mean field and numerical diffusion zones near the vertical edges of the computational domain, the mixing layer is simulated with triply periodic boundary condition, as shown in Figure 1(a). The normalised self-similar growth rates are in good agreement with published results (Figure 1(b)).

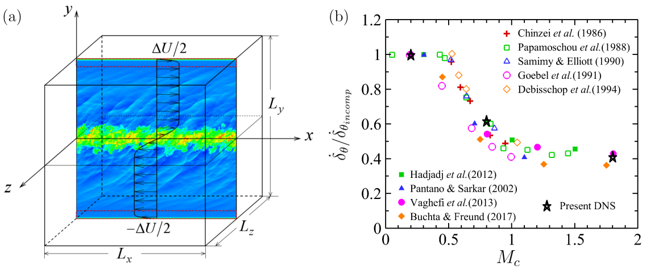
Figure 1. (a) Schematic of the temporally evolving shear layer with mean velocity profile. (b) Comparison of linear growth rates at different Mc with different numerical and experimental results.

Figure 2. Contours of instantaneous velocity fluctuations along with stronger events of viscous dissipation indicated by black solid lines: (a) streamwise; (b) vertical.

As the convective Mach number increases, the streamwise dissipation becomes more effective in suppressing the turbulent kinetic energy. At Mc = 1.8, the streamwise dissipation increases much faster than the other two components in the transition region, even larger than pressure-strain redistribution, correlating with the streamwise velocity and elongated vortical structures at a higher level of compressibility (Figure 2).

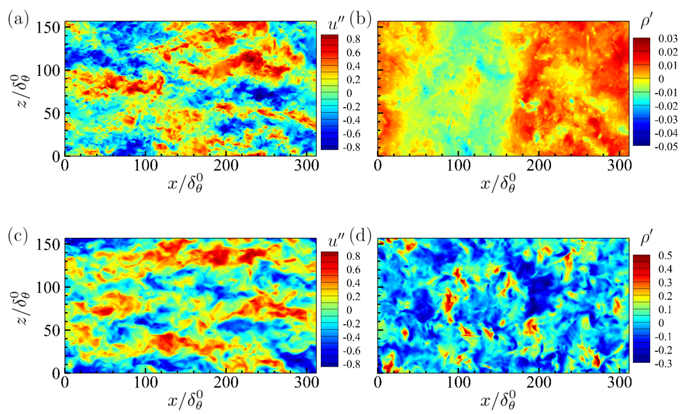
Figure 3. Instantaneous fields of the streamwise velocity and density fluctuation for cases (a), (b) M02 and (c), (d) M18 in the self-similar region.

In the self-similar region, compressibility effects on small-scale vortical structures are clearly weaker than in the transition region. Therefore, the suppression mechanism of layer growth rate due to compressibility is further examined by analysing the large-scale structures in the mixing layers. Prof. Wang’s team confirm the existence of the large-scale high- and low-speed structures in the mixing layers, which accompany the spanwise Kelvin-Helmholtz rollers at low convective Mach number and dominate the mixing layer at higher convective Mach number (Figure 3). Conditional statistics demonstrate that the large-scale low-speed structures are lifted upwards by a pair of counter-rotating quasi-streamwise rollers flanking the structures.

Figure 4 displays that the small-scale vortical structures have an apparent preference for clustering into the top of the low-speed regions. The interaction of small and large structures is directly associated with high-shearing motions on top of the low-speed structures.

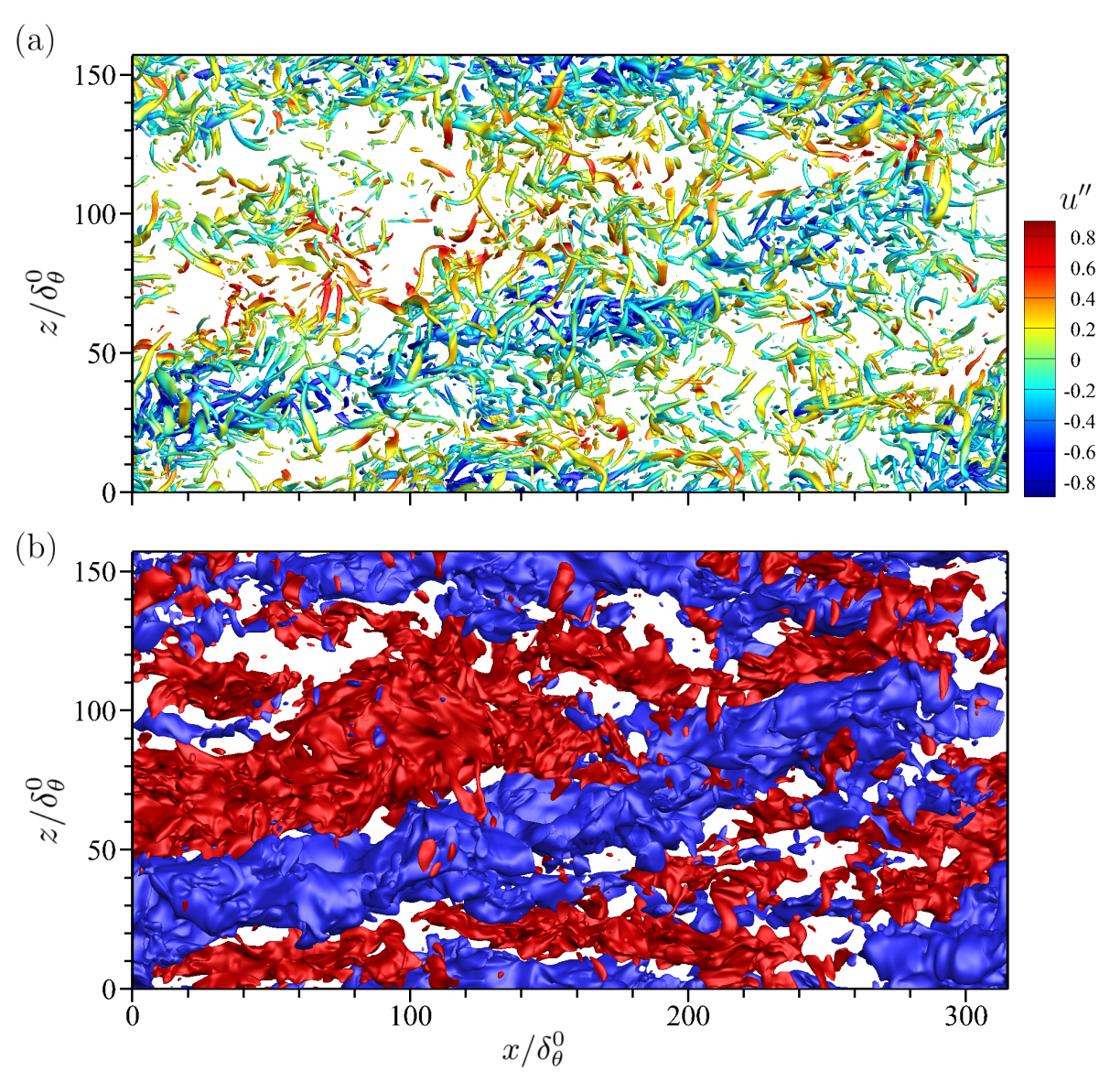
Figure 4. Top view of coherent structures in the upper half-domain for Mc = 1.8. (a) Small-scale vortical structures visualised by the iso-surfaces of Q-criterion. (b) The high- (red) and low-speed (blue) large-scale structures presented by the iso-surfaces of streamwise velocity.

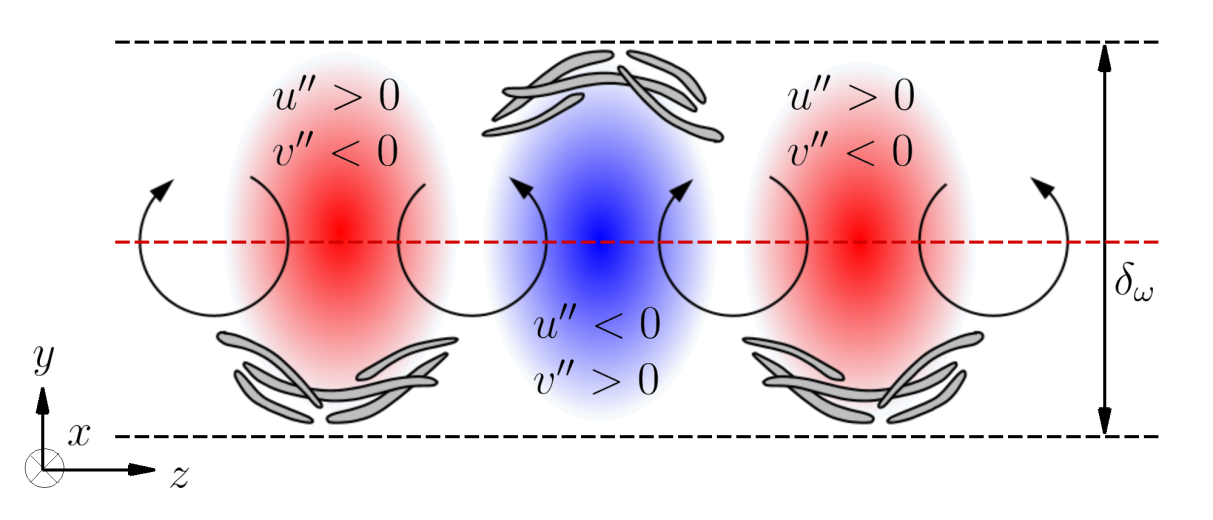
Figure 5. Schematic of large-scale coherent structures and their interaction across the mixing shear layer for higher convective Mach number Mc ≥ 0.8.

More importantly, the universality of the large-scale high- and low-speed structures in free shear and wall-bounded turbulent flows is revealed. Based on the present results, the large-scale high- and low-speed structures are reconstructed by a conceptual model which resembles the outer part of the well-known model of wall-bounded turbulent flow proposed by Marusic et al., 2010, as shown in Figure 5.

Xiaoning Wang, Research Asst. Prof. in Assoc. Prof. Jianchun Wang’s research group, is the first author of the paper. Assoc. Prof. Jianchun Wang and Prof. Shiyi Chen are the co-corresponding authors. SUSTech is the correspondence institute.

This work was supported by the Basic Science Center Program of the National Natural Science Foundation of China (NSFC), Science, Technology and Innovation Commission of Shenzhen Municipality, and Department of Science and Technology of Guangdong Province.

Paper link: https://doi.org/10.1017/jfm.2022.660

To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.