Flexible pressure sensors can convert pressure into electrical signals, and iontronic flexible pressure sensors (devices with extremely high sensitivity) have important application value in robotic haptics, automatic pilot and drive, virtual reality, and wearable healthcare. However, existing flexible pressure sensors generally suffer from signal drift, which is caused by the creep of soft materials, and for iontronic sensors, the leakage of ingredients. Therefore, the sensors often operate sensitively but not accurately, and cannot be used for precise measurement of static or quasi-static pressure, which significantly restricts the practical deployments.
Regarding the above challenges, Professor Chuan-Fei Guo from the Department of Materials Science and Engineering and Assistant Professor Canhui Yang from the Department of Mechanics and Aerospace Engineering at the Southern University of Science and Technology (SUSTech) have collaborated to develop a drift-free flexible pressure sensor, which resolves the long-standing challenge of signal drift under prolonged high static pressures.
Their paper, entitled “Creep-free polyethylene elastomer for drift-free iontronic sensing”, has been published in Nature Materials, a journal covering a range of topics within materials science.
The research team rationally designed and synthesized a leakage-free and creep-free ionic conductor, termed polyelectrolyte elastomer (PEE), at the molecular level, which effectively suppressed the signal drift of the resulting iontronic flexible pressure sensor (Fig. 1). The PEE was a copolymer consisting of charged ionic segments and neutral slippery segments (Fig. 1d). The former bonded cations to molecular chains, preventing the outward diffusion of ions through network elasticity. The latter could effectively reduce the electrostatic interactions between molecular chains, significantly reducing the creep of the material. In addition, increasing the crosslinking density further reduced the creep of the material.

Figure 1. Principles, materials, and chemistries for drift-free iontronic sensing
The design of leakage- and creep-free ionic conductors can be illustrated by various chemistries. Specifically, the PEE here was poly(1-(3-(acryloyloxy)propyl)-3-methylimidazolium bis(trifluoromethane) sulfonimide-co-methyl acrylate) (P(AMT-co-MA)), and had been further toughened by polymethyl acrylate (PMA) long chains. The final PEE was termed P(AMT-co-MA)-PMA. Subjected to a tensile stress of 200 kPa for 40000 seconds, the sample maintained its mechanical and electrical properties (e.g., tensile strain and impedance) (Fig. 2a). In addition, the performance of creep-resistance under dynamic loads was also verified.
When subjected to a triangular wave cyclic load with a peak stress of 400 kPa and a frequency of 1 Hz, the peak strain remained almost unchanged over 100000 cycles (Fig. 2b). The researcher prepared three types of PEE, with PAMT containing only charged ionic segments being represented as PEE1, P(AMT-co-MA) containing both charged ionic segments and uncharged slippery neutral segments being represented as PEE2, and P(AMT-co-MA)-PMA toughened with long-chain PMA based on PEE2 being represented as PEE3. The uniaxial tensile curves are shown in Fig. 2c. The performance of the toughened PEE3 was significantly improved, with a fracture strain of 61.3%, a tensile strength of 560 kPa (Fig. 2d), fracture energy of 323.5 J m-2 (Fig. 2e), and compressive strength of 8.2 MPa (Fig. 2f). PEE had a non-tacky surface and exhibited low hysteresis. The adhesion energy between PEE and the gold electrode was 20.78 J m-2 (Fig. 2g).
In the loading and unloading cycle test, the stress-strain curves of the first and 1000th cycles almost overlapped, resulting in an average hysteresis of <3% over 1000 cycles (Fig. 2h). The electrical performance of ionic conductors was also important. Researchers conducted ac-impedance measurements on PEE3 and plotted its Nyquist curve (Fig. 2i) and Bode phase diagram (Fig. 2j). For brevity, PEE3 was abbreviated as PEE in the following.
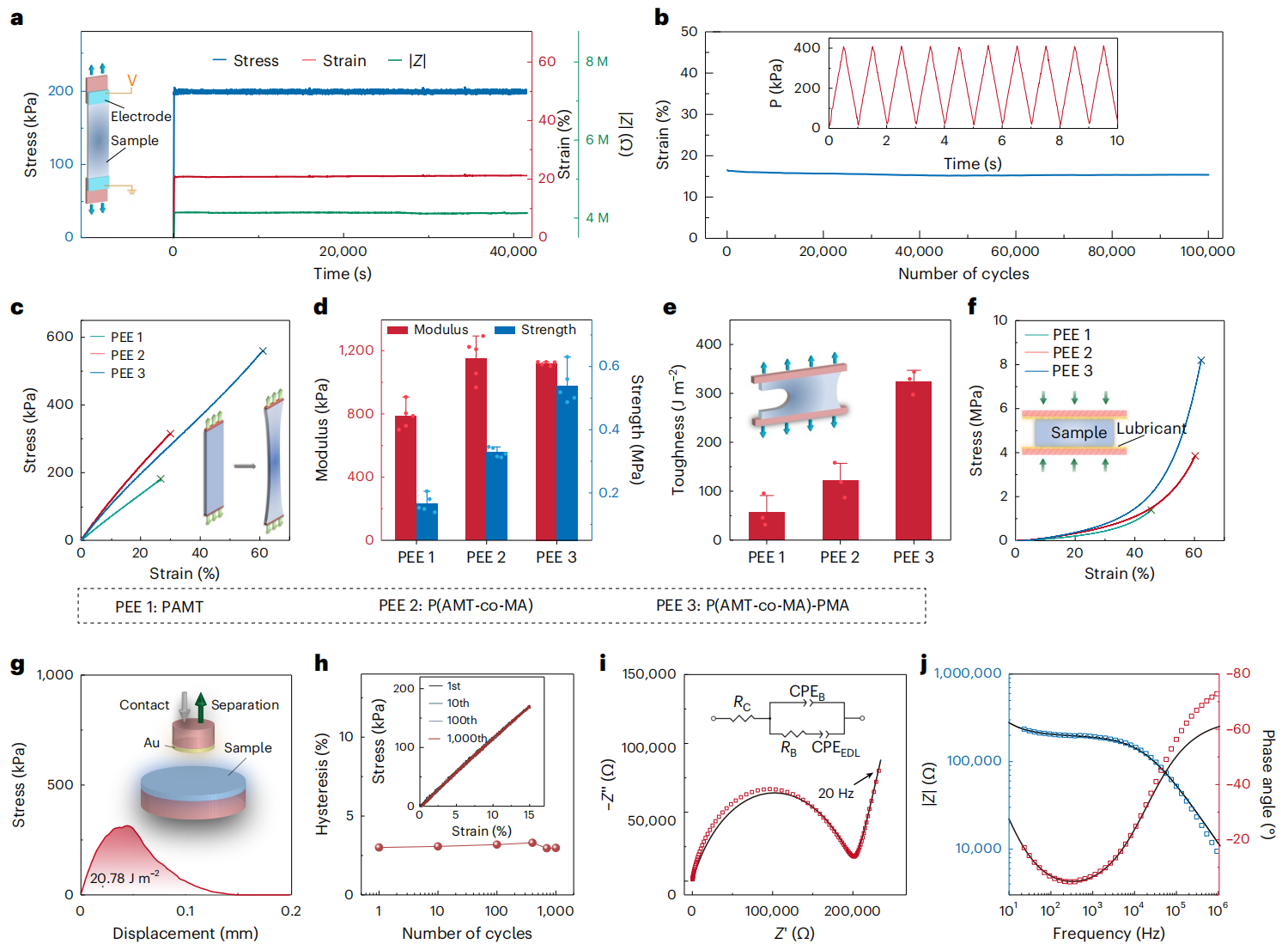
Figure 2. Characterizations of the polyelectrolyte elastomer
The researcher constructed the sensor by sandwiching a layer of PEE between two layers of gold electrodes (Fig. 3a). When subjected to a sudden load of 2.5 kPa, the response time of the sensor was about 3.8 ms, and the recovery time was about 5.8 ms (Fig. 3b). Sensors exhibited high sensitivities in the range of 0-1000 kPa (Fig. 3c). Subjected to a static pressure of ~500 kPa, the capacitance drift was less than 1% within 48 hours (Fig. 3d). Subjected to a cyclic load of 400 kPa with square-waves, the sensor output square-wave signals accordingly for each cycle over a total of 1000 cycles (Fig. 3e).
The team also validated the drift-free performance of the sensor in more complex situations by overlaying a periodic fluctuation of 50 kPa on a static pressure of 375 kPa, and the response of the sensor was in phase with the stimulus (Fig. 3f). They selected the widely used ionic conductor (PVDF-HFP)-[EMIM][TFSI] for comparison. Under the static compression of 500 kPa, the capacitance drifted about 102.9% in 10 minutes (Fig. 3g). Its signal also drifted in a cyclic load using square waves (Fig. 3h), or in the case of superposed static and dynamic compression (Fig. 3i).
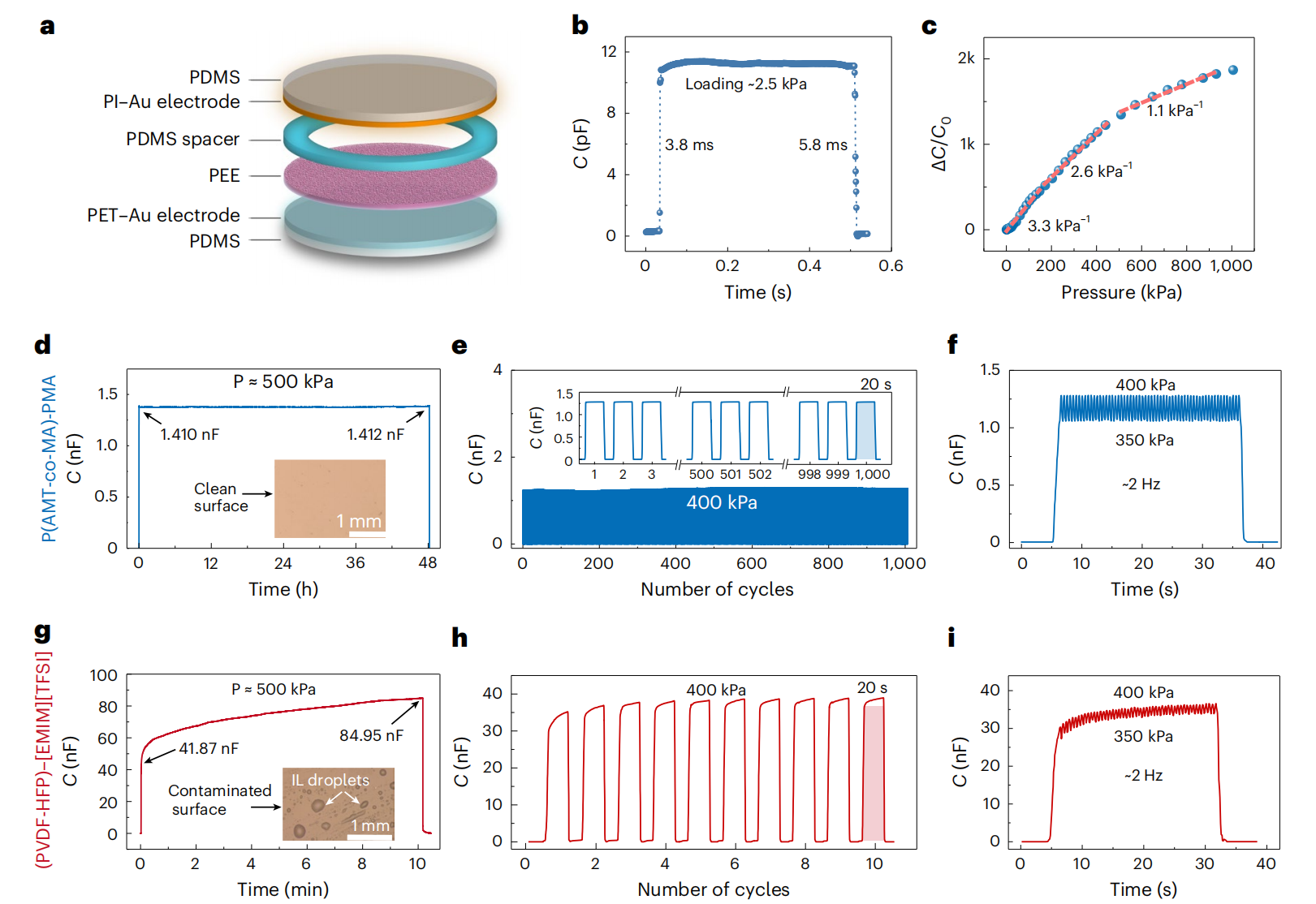
Figure 3. Sensing properties of the iontronic sensor
The researchers proposed two indicators, drift ratio and drift rate, to quantitatively characterize the signal stability under static pressure (Fig. 4a). They made ten kinds of sensors, whose ionic conductors were the optimized PEE, three kinds of unoptimized PEE, four kinds of ionogel, one kind of hydrogel and one kind of solvent-free ionic elastomer. Tested at 500 kPa for 10 minutes, the sensor based on the optimized PEE showed an average drift ratio of approximately 0.33% within 10 minutes, which was two orders of magnitude lower than all other sensors (Fig. 4b). In addition, the drift rate of sensors based on the optimized PEE at 500 kPa was at least 2-4 orders of magnitude smaller than that of other sensors (Fig. 4c).
They calculated the ratio of pressure to its modulus (P/E) when the sensors exhibited drift behavior to characterize the allowable pressure that a sensor could work without signal drift. Sensors based on the optimized PEE could work at a P/E of 0.45, while the sensors using traditional soft materials only achieved drift-free sensing at a low P/E below 10-4, and the silicon-based sensors had an allowable P/E of about 10-3 (Fig. 4d).
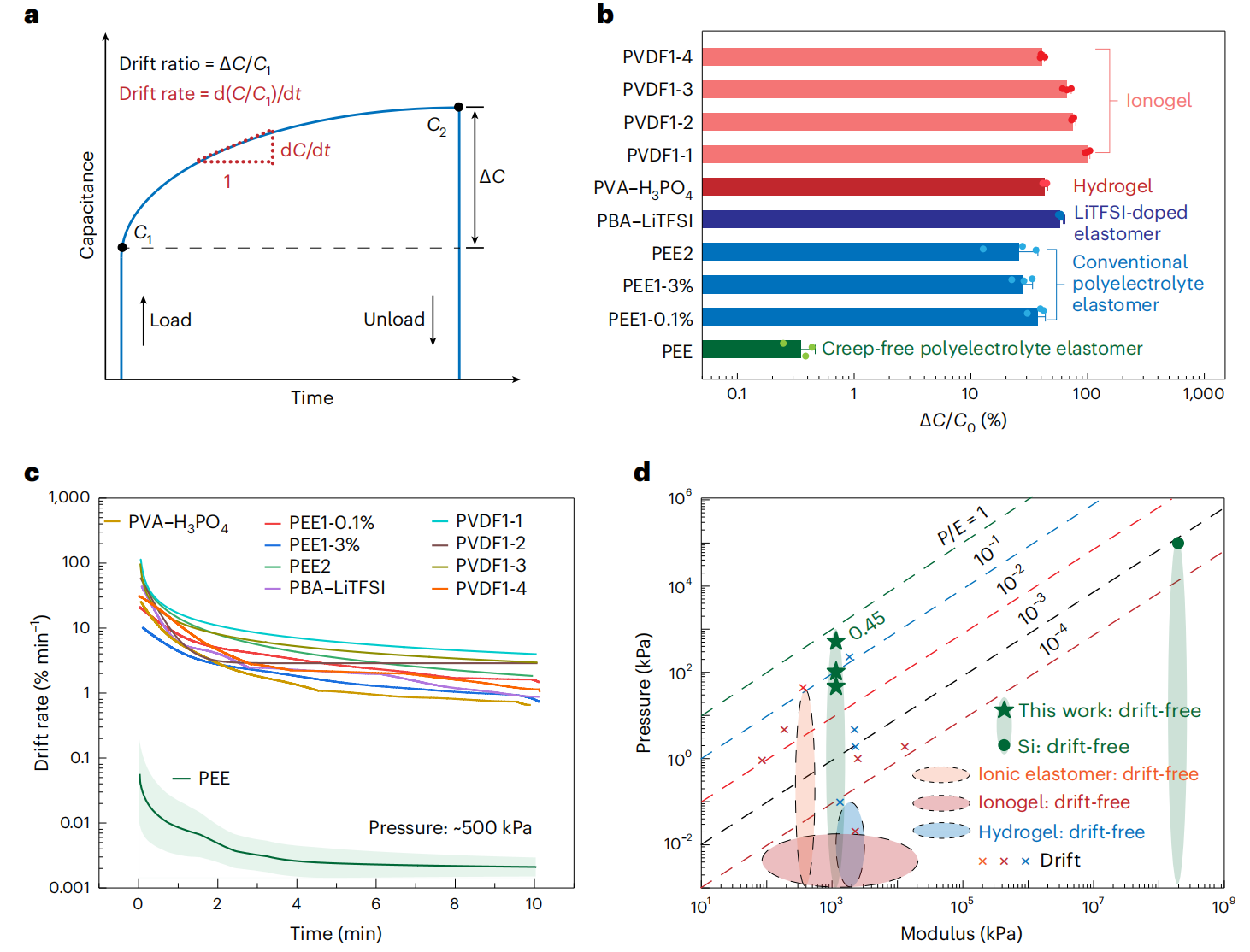
Figure 4. Drift ratio and drift rate of various iontronic sensors
The sensor was integrated with a robotic gripper, which was driven by a motor and equipped with a commercial sensor for force monitoring (Figure 5a). Using an Arduino board to drive a motor to change the degree of gripper closure (DGC) of the robotic gripper, the researchers used the sensor signal as the input to control the DGC using a PID program (Figure 5b). They demonstrated the precise control of the robotic gripper with drift-free sensors, which could stably grasp steel blocks under a high clamping pressure of 350 kPa for 20 minutes, during which the DGC and clamping force remained stable (Figure 5c, d). In contrast, when the ionogel-based sensor was integrated into the robotic gripper, the PID program continuously adjusted the DGC under a fixed pressure of 350 kPa, resulting in the slip-off of the steel block (Figure 5e).
Owing to the precise detection of force using the drift-free sensors, the robotic grippers could safely catch fragile objects. This was demonstrated with a stable grasping of a cherry tomato for 1500 seconds (Figure 5f). In contrast, when a hydrogel-based sensor was used, the dehydration of the hydrogel led to the reduction of the electrical signal, which led to the increase of the DGC. Finally, it crushed the cherry tomato (Fig. 5g). Drift-free sensing of soft, flexible pressure sensors has tremendous applications, particularly in cutting-edge technologies such as electronic skins, wearable devices, humanoid robots, and beyond.
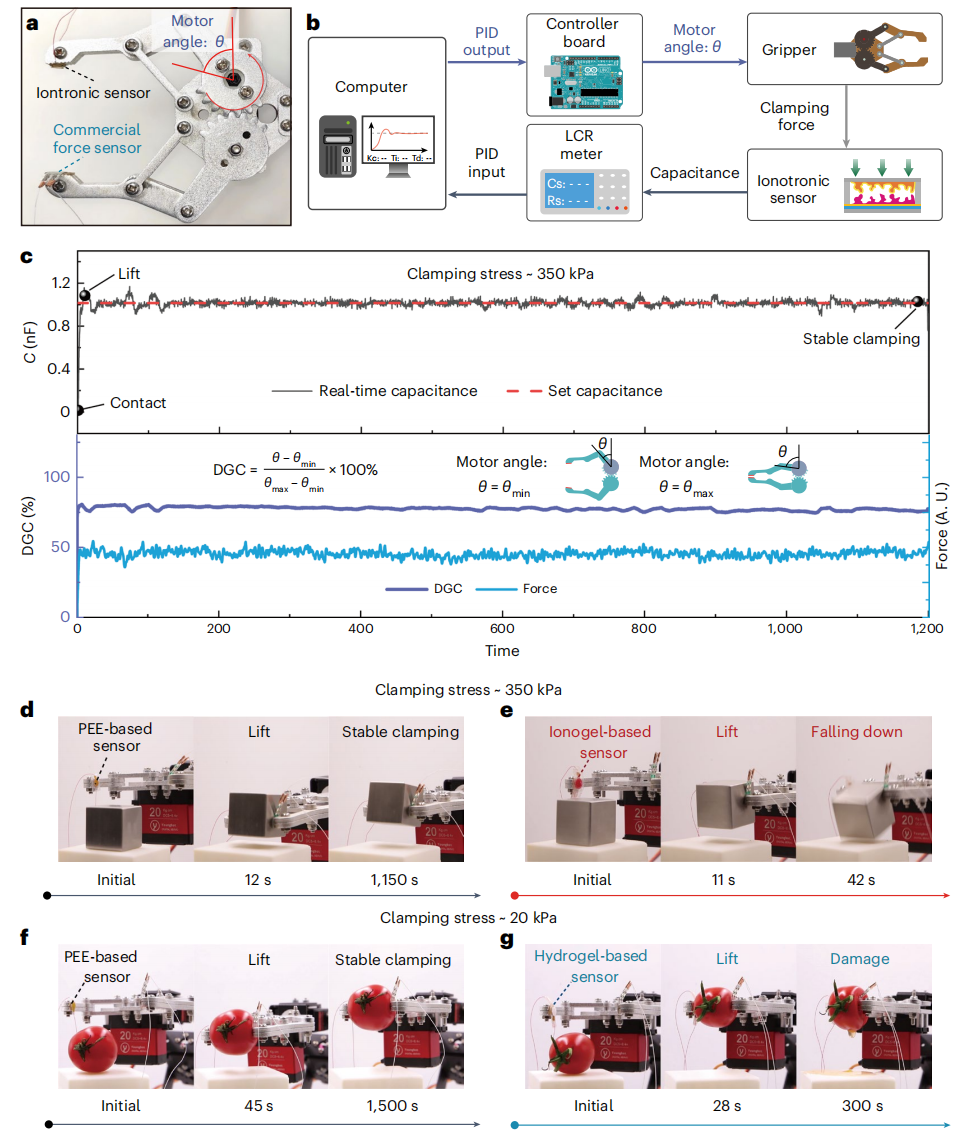
Figure 5. Accurate force sensing for steady robotic manipulation
Yunfeng He, a doctoral candidate from the Department of Mechanics and Aerospace Engineering, and Yu Cheng, a doctoral candidate from the Department of Materials Science and Engineering, are the co-first authors of the paper. Professor Chuan-Fei Guo and Assistant Professor Canhui Yang are the co-corresponding authors, and SUSTech is the sole affiliated institution.
This work was supported by the National Natural Science Foundation of China (NSFC), Science and Technology Department of Guangdong Province, and the Shenzhen Science and Technology Innovation Commission.
Paper link: https://www.nature.com/articles/s41563-024-01848-6
To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.
Proofread ByAdrian Cremin, Yingying XIA
Photo By