In the early 1970s, Prof. Alan G. Hawkes proposed the self/mutual-exciting process in his studies. A non-Markovian self-excited point process with long memory effects can capture a feature that any historical event will affect the probability of future events for a long time and may lead to critical bursts. Hawkes process is an example of such a process.

An event in the Hawkes process can be a burst of electrons in an amorphous semiconductor or an organic compound associated with photoconductivity. Such events could be an earthquake, an epidemic, an epileptic seizure, a financial volatility burst, a book sale, a view of a YouTube video, or any other occurrence in social dynamics.

Prof. Didier Sornette’s group at the Institute of Risk Analysis, Prediction, and Management (Risks-X) of the Southern University of Science and Technology (SUSTech) Academy for Advanced Interdisciplinary Studies has recently published their latest results on the theory of self-exciting Hawkes Process and its nonlinear generalization in Physical Review Letters.

In 2021, the group has published three papers in Physical Review Letters and two papers in Physical Review Research on the theoretical progress of the Hawkes process.

The linear self-exciting Hawkes point processes are first-order non-Markovian stochastic models of intermittent burst dynamics. Nonlinear Hawkes processes have been introduced to describe the co-existence of excitatory (or positive feedbacks) and inhibitory effects (or negative feedbacks).

Although nonlinear Hawkes processes have been applied in many fields, obtaining analytical solutions of these models is very difficult due to the complex interplay between their nonlinear and non-Markovian structures. The non-Markovian structure of the models has been an obstacle to the development of a unified theoretical framework for analysis, which has led to the general form of nonlinear Hawkes processes hardly being studied.

On the other hand, the origin(s) of the ubiquity of probability distribution functions (PDF) with power-law tails

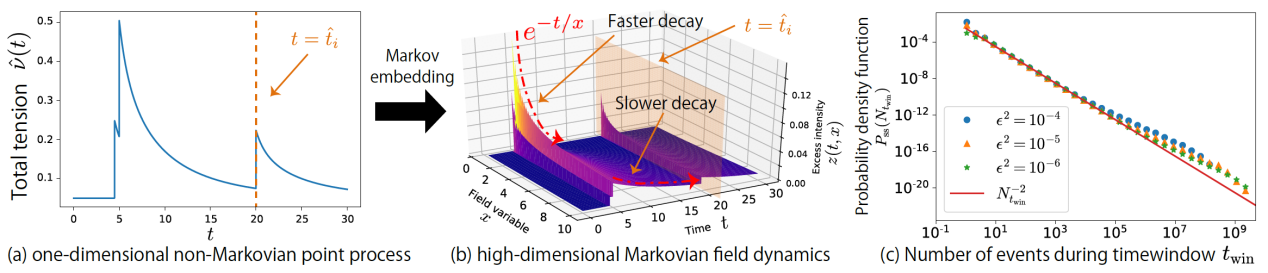
Figure 1. Schematic of the Markov embedding from the one-dimensional non-Markovian process to the infinite-dimensional Markovian field dynamics.

Motivated by activation processes of the Arrhenius form, Prof. Sornette’s group brings the two threads together by introducing a general class of nonlinear self-excited point processes with fast-accelerating intensities as a function of “tension”.

Using the Markov embedding method previously developed by his group, this paper presents various exact and robust asymptotic solutions of the nonlinear Hawkes process using the field master equation. This paper also presents a general formulation for the nonlinear Hawkes processes and provides straightforward solutions for various cases.

In particular, they report three interesting asymptotic features valid for a broad class of memory kernels. Solving the corresponding master equations, they found that a broad class of such nonlinear Hawkes processes has the PDF of their intensities described by a power law. Their theoretical finding suggests the nonlinear self-excited mechanism as an explanation for the universality of power laws.

In particular, Zipf’s scaling naturally appears when the distribution of marks is symmetric. This unearths a novel mechanism for power laws, including Zipf’s law, providing a new understanding of their ubiquity. Since nonlinear Hawkes processes may have a huge variety of forms, and consequently control parameters, it would be useful to further study various nonlinear Hawkes processes by systematically classifying their solutions according to the asymptotic analysis of the field-master equations.

Prof. Kiyoshi Kanazawa from the University of Tsukuba, Japan, is the first author of this paper. Prof. Didier Sornette, a member of the Academia Europaea, is the corresponding author.

This work was partly supported by the National Natural Science Foundation of China (NSFC).

Didier Sornette’s group has achieved a series of groundbreaking results in both theoretical and applied research on Hawkes processes. For further review of these studies, please see the links at the end of the page.

Paper links:

Physical Review Letters (October 2021):

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.188301

Physical Review Research (October 2021):

https://arxiv.org/abs/2110.01523

Previous paper links:

Physical Review Letters (September 2020):

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.138301

Physical Review Research (September 2020):

https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.2.033442

To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.