In analogy with the crucial brake of a running car, a brake for photons is also extremely important to control the photon dynamics. Similar to the basic principle of car brakes, injecting losses into an excited optical cavity could hasten the otherwise slowly relaxed photons to a steady state. Compared to the conventional brake of a car, photon brake is applied in the timescale of picosecond or femtosecond.

Associate Professor Longqing Cong from the Department of Electrical and Electronic Engineering at the Southern University of Science and Technology (SUSTech) and collaborators explored the effects of “photon brake” with metamaterials by using an optical pump terahertz probe (OPTP) spectroscopic system.

Their study, entitled “Temporal loss boundary engineered photonic cavity,” was published in Nature Communications. It would provide solutions for ultrafast beam scanning with metasurfaces, benefiting the development of Lidar and terahertz wireless communications.

Loss is ubiquitous and unavoidable in nature, inhibiting most optical processes’ performance. A similarity to applying controllable friction to a car for braking, it is feasible to inject loss into an excited photonic cavity to manipulate the oscillating time of photons. This mission is tricky because the timing to control photons is fleeting in the scale of picosecond (10^-12 s) or even femtosecond (10^-15s).

In this work, photon brake is realized by injecting photocarriers into semiconductor cavities through femtosecond laser pulses whose injection timing and intensity could be adjusted accurately so that they can manipulate photons like a free-wheeling car.

The dynamics of excited photons by probe pulse is interpreted in the time domain as the long-lasting oscillations whose oscillating time is determined by the mode quality factors (Q) (Fig. 1a-1c). In the period of oscillation, the researchers could inject photocarriers at a specific instant with a controllable concentration (dashed lines in Fig. 1c). The dynamics of photons are disturbed along with a series of interesting phenomena.

The perturbation of photon brake is visualized in the frequency-domain spectra (red line in Fig. 1d). Two spectral features are observed. Firstly, asynchronous modulation of the two modes with only the transverse electric (TE) mode modulated, leaving the transverse magnetic (TM) mode unaffected. Secondly, a spectral “ripple” is generated. The asynchronous modulation process is studied in detail (Fig. 1f, in contrast to the spectral evolution in Fig. 1e and the blue line in Fig. 1d), which exhibits the quantitative dependence of asynchronous modulation on Q of the two modes. The second spectral feature originates from the perturbation of Lorentzian lineshape of TE mode due to the sudden injection of transient loss that will introduce new frequency components.

Figure 1. (a-c) Interpretation of photon brake from time-domain oscillations. (d-f) Interpretation of photon brake in the frequency domain with two interesting spectral features.

The typical spectral features are observed in experiments by the optical pump terahertz probe (OPTP) setup. A temporal two-dipole model is proposed, which involves the physical process of transient loss injection and quantitively reproduces all the experimental observations (Fig. 2b-d).

Coupled cavity photons can be distinguished by stripping one photonic mode through controlling the transient loss boundary, which is inaccessible by any other means and enables the transition from a coupled to an uncoupled state. The mode stripping threshold is characterized by the spectral transition between underdamped and overdamped states (Fig. 2a).

In addition to the modulation of the imaginary part of the refractive index in the process of transient photocarrier injection, the correlated transient modulation of the real part also occurs. The sudden change of the real part of the photonic cavity will lead to the shift of photon frequency, an analogy to changing a guitar’s tone by adjusting the string length after plucking. This frequency conversion process is linear and would provide a solution for terahertz frequency conversion.

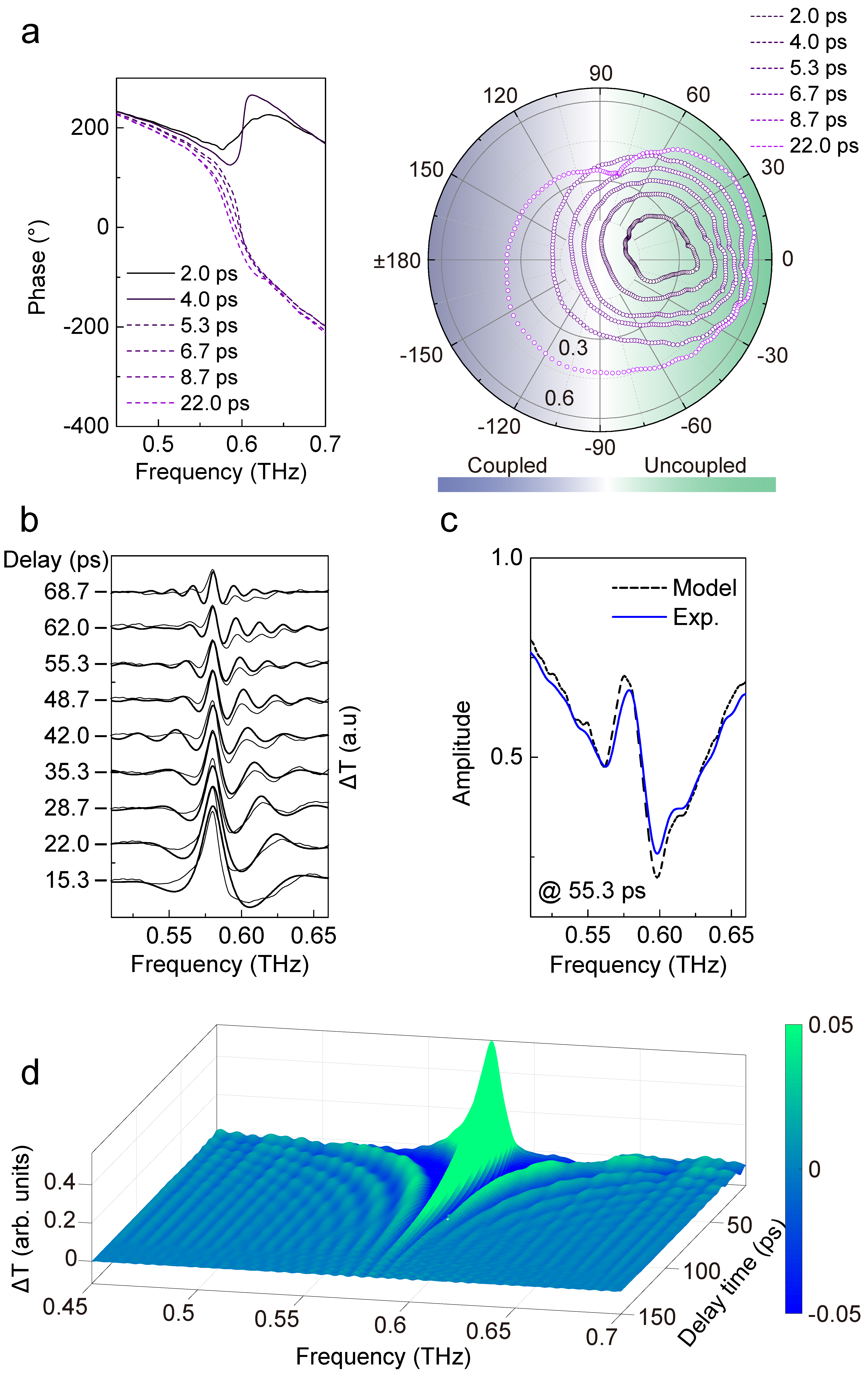
Figure 2. (a) Phase spectra and the parametric polar plot of transmission for the cavity at various delays. (b-d) Transient two-dipole model to reproduce experimental phenomena.

Associate Professor Longqing Cong from SUSTech is the corresponding author of this paper. This work was mainly supported by SUSTech and was funded by the National Natural Science Foundation of China (NSFC).

As the principal investigator of the Tera-Meta team, Prof. Longqing Cong is currently recruiting graduate students and postdocs with a background in physics, optics, optoelectronics, materials, and communications to work on terahertz and metamaterials. For further details, please follow the link below.

Related links:

Nature Communications: https://www.nature.com/articles/s41467-021-27014-z

Recruitment Information: https://eee.sustech.edu.cn/?view=%e4%b8%9b%e9%be%99%e5%ba%86&jsid=18&lang=en

To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.