Spin space groups offer a comprehensive framework for understanding the intricate magnetic geometry of magnetic materials, extending beyond traditional crystallographic and magnetic group theories. Research in this area is crucial because it addresses the limitations of existing magnetic group theories, providing a deeper insight into the physical properties and behaviors of magnetically ordered materials. This advanced understanding is essential for developing innovative applications in solid-state physics, semiconductor science, and materials engineering. Moreover, exploring spin space groups can unveil new magnetic phenomena and emergent behaviors, paving the way for groundbreaking discoveries in material science and technology.

Professor Qihang Liu’s research group from the Department of Physics at the Southern University of Science and Technology (SUSTech) has recently made progress in the study of spin space groups, which describes the magnetic geometry of magnetic materials.
Their results, entitled “Enumeration and representation theory of spin space groups”, have been published in the journal Physical Review X.
In the realm of physics and materials science, symmetry has always played a central role. Since the late 19th century, scientists have embarked on the exploration of crystal symmetry and developed a fundamental framework known as crystallographic group theory. This theory describes the properties and behaviors of crystalline solids, using 32 crystallographic point groups and 230 crystallographic space groups. Central to the essence of crystallographic group theory is the depiction of symmetry elements in three-dimensional non-magnetic or paramagnetic solids, encompassing rotations, inversions, reflections, translations, and their combinations.
In the early 20th century, the theory of space groups was further developed, and scientists became aware of the existence of additional symmetries in magnetic materials beyond the already-known geometric symmetries. These additional symmetries are associated with the magnetic moments of the atoms or ions present in these materials. In the mid-20th century, Soviet crystallographer Alexei V. Shubnikov and others extensively researched the symmetries of magnetic materials. They introduced anti-symmetry into the theory of space groups and proposed the concepts of magnetic point groups and magnetic space groups. These groups include not only geometric symmetry operations but also operations that flip the spins, providing a new perspective for analyzing the symmetries of magnetic materials.
Establishing theories on crystallographic and magnetic groups has not only enhanced our understanding of various characteristics of crystals, but has also been instrumental in driving the rapid advancement of fields like solid-state physics, semiconductor science, and materials engineering.
Although the magnetic group theory is often regarded as a universal theory that describes the geometric characteristics and physical properties of all magnetically ordered materials, further research on magnetic materials has led to the recognition of the necessity for a more comprehensive group that can fully characterize their magnetic geometry and physical properties. This recognition arises from the fact that the spin magnetic moment, as an intrinsic degree of freedom of the material, possesses a rotational vector property in addition to flipping. As a result, the symmetry operations in spin space can exist independently of the lattice symmetry operations without considering the coupling with the lattice space.
A representative example is the breaking of spin SU(2) rotational symmetry observed during the paramagnetic-ferromagnetic transition in a crystal. In magnetic groups, the rotation of spins and lattices is inextricably linked. Consequently, to provide a complete description of the configuration of magnetically ordered materials, it is necessary to separately consider the symmetry operations in lattice and spin space (as shown in Figure 1). This consideration leads to the larger groups known as the spin groups, encompassing both the spin point and the spin space groups.
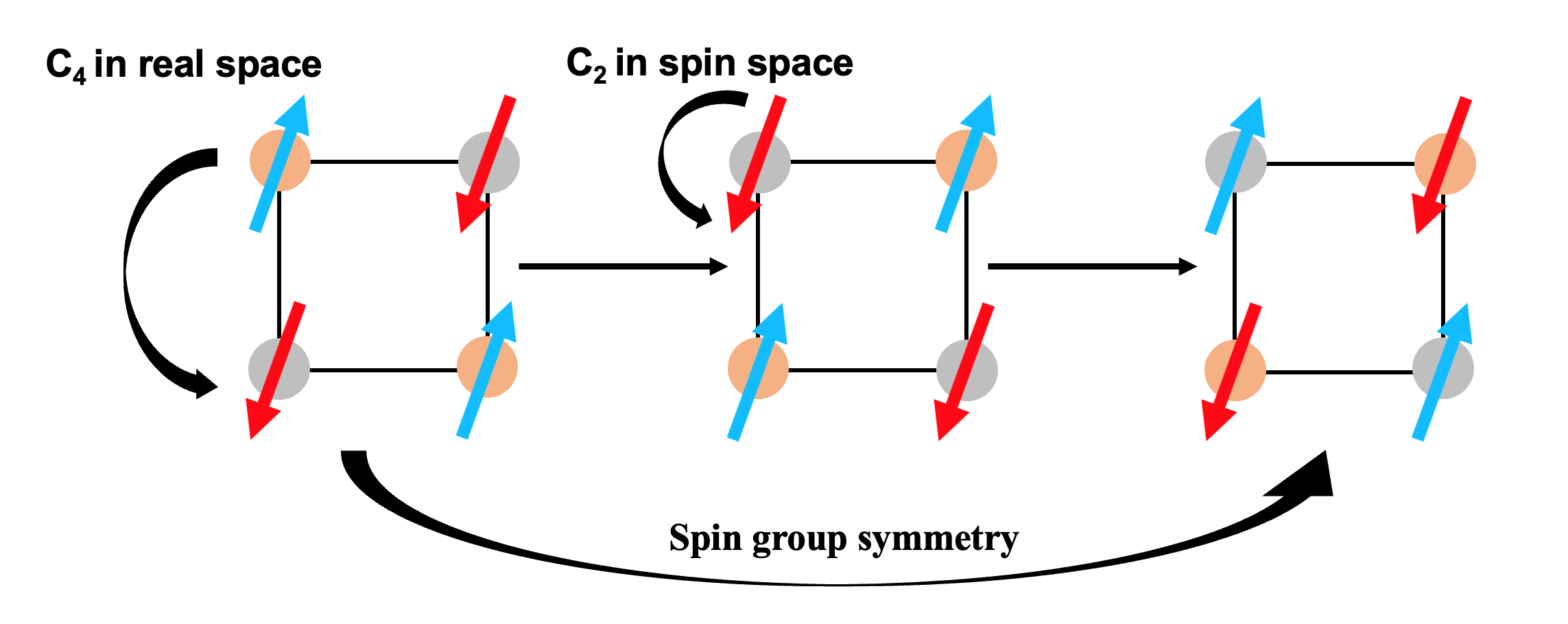
Figure 1. An example of spin-group symmetry, where a four-fold rotation in real space is combined with a two-fold rotation of the spin in spin space
The theory of crystallographic and magnetic groups has been well-established for several decades and is extensively covered in textbooks. In contrast, research on spin groups, particularly the fundamental theory of spin space groups, is still in its nascent stages both domestically and internationally.
In the 1970s, Daniel B. Litvin’s group from the University of Pennsylvania enumerated 598 spin-point groups. Starting from 2021, Professor Qihang Liu’s research group has focused on two research directions: the development of the new theoretical framework and the prediction of novel effects related to spin groups, and they have achieved some progress in these areas. Their accomplishments include the classification of spin point groups for collinear, coplanar, and non-coplanar magnetic structures (Phys. Rev. X 12, 021016 (2022)); enhanced spin-orbit coupling effects in magnetic materials (Nat. Commun. 13, 919 (2022)); chiral Dirac fermions (The Innovation 3, 100343 (2022)); and the discovery, in collaboration with Professor Chang Liu from the Department of Physics at SUSTech, of antiferromagnetic spin splitting for the first time (Nature 626, 523 (2024)).
Regarding spin space groups, the interplay between crystal translations and spin rotations adds greater challenges to the study of their classification and representation theory. In this work, the researchers accomplished several significant tasks related to the expansion of the spin space group and its enumeration and representation theory. Starting from 230 crystallographic space groups and finite translation groups with a maximum order of eight, a complete enumeration set containing over 100,000 spin space groups was established. They also developed international symbols for all spin space groups, making it convenient to directly interpret all symmetry operations from the group symbols.
Additionally, the team created an online program, FINDSPINGROUP, to identify the spin group and magnetic group symmetries of any magnetically ordered crystal. This tool also helps analyze related physical effects such as spin splitting, the anomalous Hall effect, and quantum geometry. Lastly, they developed the representation theory of spin space groups, which characterizes the irreducible corepresentations of wave-vector little groups in the momentum space of quantum state wave functions.
This work not only advances the theory of symmetry in describing magnetically ordered materials, but also opens up new avenues for understanding and exploring emergent phenomena in magnetic materials. Through several representative examples, including the additional band degeneracy in the candidate altermagnet RuO2, the spiral spin polarization in the spiral magnet CeAuAl3, and the geometric Hall effect in the noncoplanar antiferromagnet CoNb3S6, the research group demonstrated how to understand novel physical effects beyond the framework of magnetic groups through the analysis of spin group symmetry.
The first authors of the paper include postdoctoral researcher Xiaobing Chen from the Department of Physics (currently an Associate Researcher at the Quantum Science Center of Guangdong–Hong Kong–Macao Greater Bay Area), master’s students Jun Ren and Yutong Yu from the Department of Physics, and Ph.D. student Yanzhou Zhu from the Department of Mathematics, all from SUSTech. Other collaborators include Chair Professor Caiheng Li from the Department of Mathematics at SUSTech. Professor Qihang Liu is the corresponding author, and SUSTech is the primary affiliation of the paper.
This work was supported by the National Key R&D Program of China, National Natural Science Foundation of China, Key-Area Research and Development Program of Guangdong Province, Guangdong Provincial Key Laboratory, Guangdong Innovative and Entrepreneurial Research Team Program, Shenzhen Science and Technology Program, and the China Postdoctoral Science Foundation.
Paper link: https://journals.aps.org/prx/pdf/10.1103/PhysRevX.14.031038
To read all stories about SUSTech science, subscribe to the monthly SUSTech Newsletter.
Proofread ByAdrian Cremin, Yingying XIA
Photo By