近日，南方科技大学电子与电气工程系高振副教授课题组在三维声学拓扑绝缘体领域取得重要进展，相关成果以“三维声学拓扑绝缘体中的多层级嵌套狄拉克锥观测”（Observation of Dirac Hierarchy in Three-Dimensional Acoustic Topological Insulators）为题发表在国际物理学著名学术期刊《物理评论快报》（Physical Review Letters）上，并被遴选为当期编辑推荐 （Editors’ Suggestion）。

      自从在石墨烯和拓扑绝缘体中观测到线性简并的狄拉克锥，狄拉克锥就以其独特的物理特性展现出许多奇异的物理现象，比如克莱茵隧穿、零折射率和鲁棒拓扑输运等。同时，破缺狄拉克锥通常会伴随着材料拓扑相的转变, 为人工调控波传输提供许多鲁棒的方式和手段。最近的理论研究发现能够在不同维度上实现“俄罗斯套娃”似的狄拉克色散。初始材料具有一个八重简并的体态狄拉克锥, 破缺对称性打开体态狄拉克锥后将在材料表面获得一个四重简并的拓扑表面态狄拉克锥, 再次打开表面态狄拉克锥后将在材料的棱上获得一个二重简并的拓扑棱态狄拉克锥, 进一步打开该棱态狄拉克锥后将获得一对二重简并的拓扑角态。该方法为实现具有丰富拓扑相变的高阶拓扑材料提供了新思路。

高振团队首次在三维声学拓扑绝缘体中实验观测到多维度、多层级嵌套狄拉克锥现象。团队首先将二维六角蜂窝声学晶体沿面外方向周期堆叠形成具有八重简并体态狄拉克锥的三维声学晶体。以此基本结构为出发点，逐渐破缺面外和面内特定的对称性，依次可得到四重简并狄拉克锥拓扑表面态、二重简并狄拉克锥拓扑棱态以及二重简并拓扑角态。借助3D打印技术，团队加工了各种对称性破缺诱导的一阶、二阶和三阶声学拓扑绝缘体，并通过声场测量揭示了多层级嵌套狄拉克锥。本研究不仅建立了一个探索狄拉克物理和高阶拓扑态的平台，而且为多维度声波鲁棒调控开辟了一条新的道路。

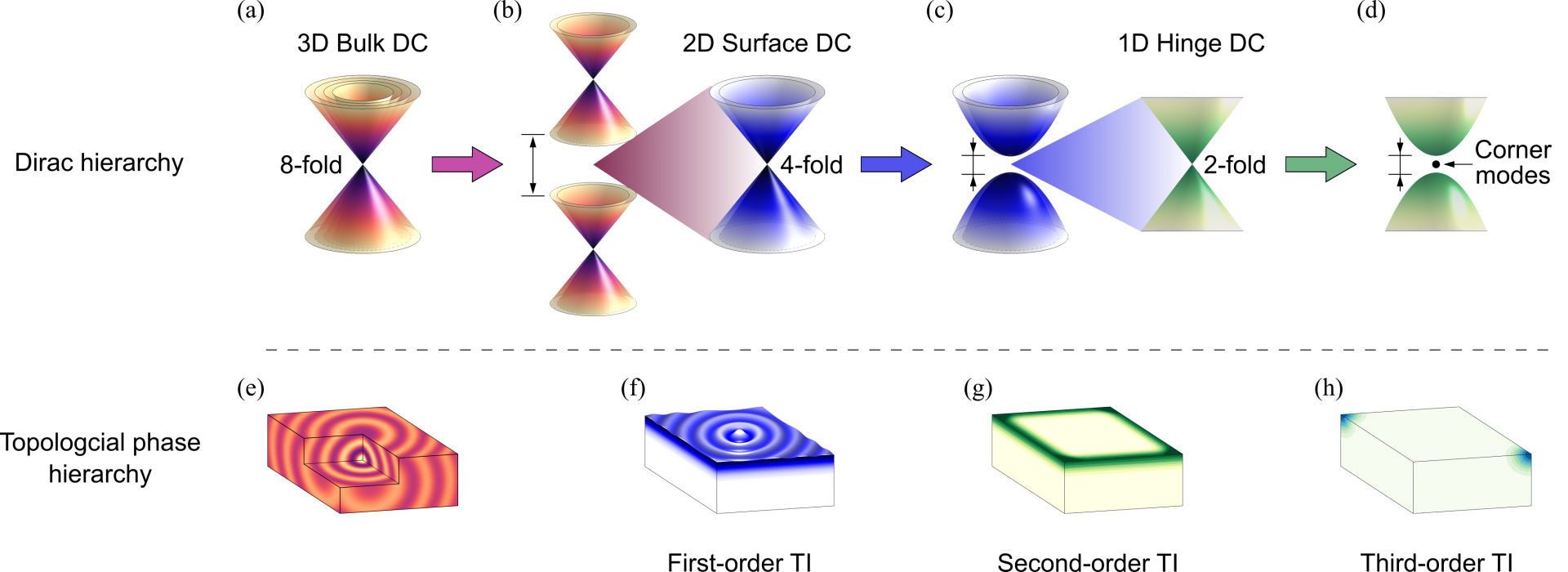
图1，多层级嵌套狄拉克锥及多阶拓扑态。多层级嵌套狄拉克锥包括（a）八重简并体态狄拉克锥（b）一阶三维声学拓扑绝缘体中的四重简并拓扑表面态狄拉克锥（c）二阶三维声学拓扑绝缘体中的二重简并拓扑棱态狄拉克锥（d）三阶三维声学拓扑绝缘体中的一对二重简并拓扑角态。多阶拓扑相包括（e）无带隙相（f）一阶拓扑相（g）二阶拓扑相（h）三阶拓扑相。

图1展示了本论文主题“三维声学拓扑绝缘体中多层级嵌套狄拉克锥”的基本物理原理。从图1(a) 所示的体态八重简并狄拉克锥出发，通过调节面内和面外的耦合系数可以依次打开体带隙得到具有四重简并狄拉克锥表面态的一阶拓扑绝缘体 [图 1(b)]，打开表面态带隙得到具有两重简并狄拉克锥棱态的二阶拓扑绝缘体 [图 1(c)]，以及打开棱态带隙后得到具有局域拓扑角态的三阶拓扑绝缘体 [图 1(d)]。图 1(e)-(h) 展示了与各层级狄拉克锥对应的无带隙相、一阶拓扑相、二阶拓扑相和三阶拓扑相。

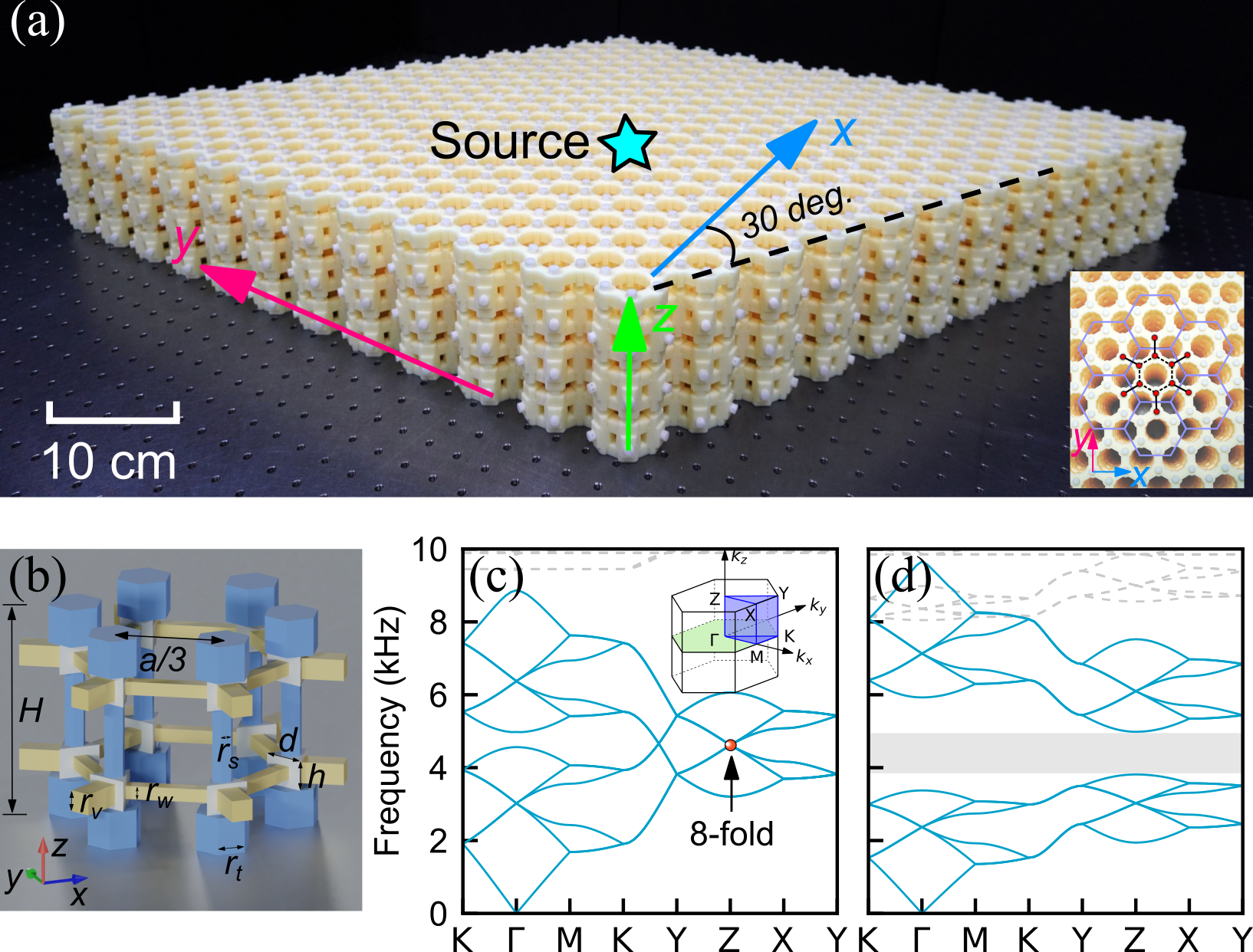
图 2：(a)一阶三维声学拓扑绝缘体样品。(b) 单胞结构，(c) 八重简并体态狄拉克锥， (d) 对称性破缺后的三维声学全带隙

图2 (a) 展示了利用3D打印技术加工的一阶三维声学拓扑绝缘体样品，其单胞结构示意图如图2 (b) 所示。图2 (c) 和 图2 (d) 分别为仿真计算的八重简并体态狄拉克锥能带和引入面外对称性破缺后打开的具有三维完全带隙的体能带。图2 (d) 所示的三维完全带隙内存在四重简并拓扑表面态狄拉克锥（见图3）。

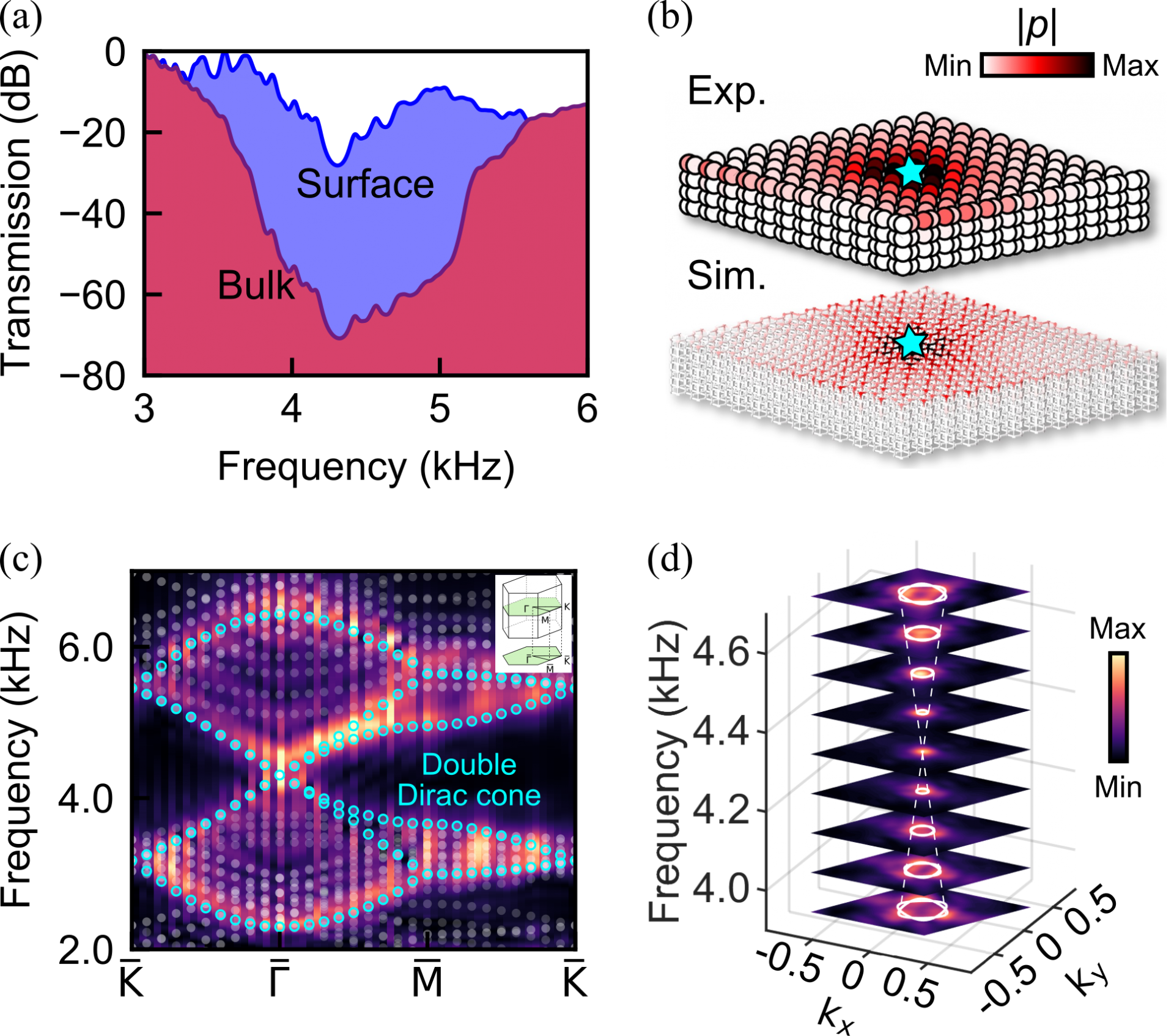
图 3：(a) 体态和表面态的实验传输谱。(b) 拓扑表面态声压分布实验及仿真结果。(c) 四重简并狄拉克锥拓扑表面态色散实验及仿真结果。(d) 四重简并狄拉克锥拓扑表面态等频带实验及仿真结果 

通过声学实验测量，图3 (a) 给出了一阶三维声学拓扑绝缘体的体态和表面态的实验传输谱，可以看到在3.8-5.0 kHz频带内，体态传输谱具有非常大的衰减，与图2(d) 中理论计算的三维全带隙相吻合。相反，在三维全带隙频率范围内拓扑表面态始终保持较高的传输率，表明在样品表面存在无能隙拓扑表面态。图3 (b) 给出了4.4 kHz频率处拓扑表面态的声场实验结果和仿真结果，可以看到声压分布只局域在样品的上表面。通过傅里叶变换将实验获得的声场分布从实空间变换到倒空间，提取到如图3 (c) 所示的实验能带结果 (背景色)。从实验结果中可以明显看到拓扑表面态的四重简并狄拉克锥，而且和仿真结果（圆圈）相吻合。图3 (d) 展示了拓扑表面态从3.9到4.7 kHz的二维倒空间中等频线分布的实验测量结果和计算结果，更加清楚的展示了拓扑表面态的四重简并狄拉克锥特征。

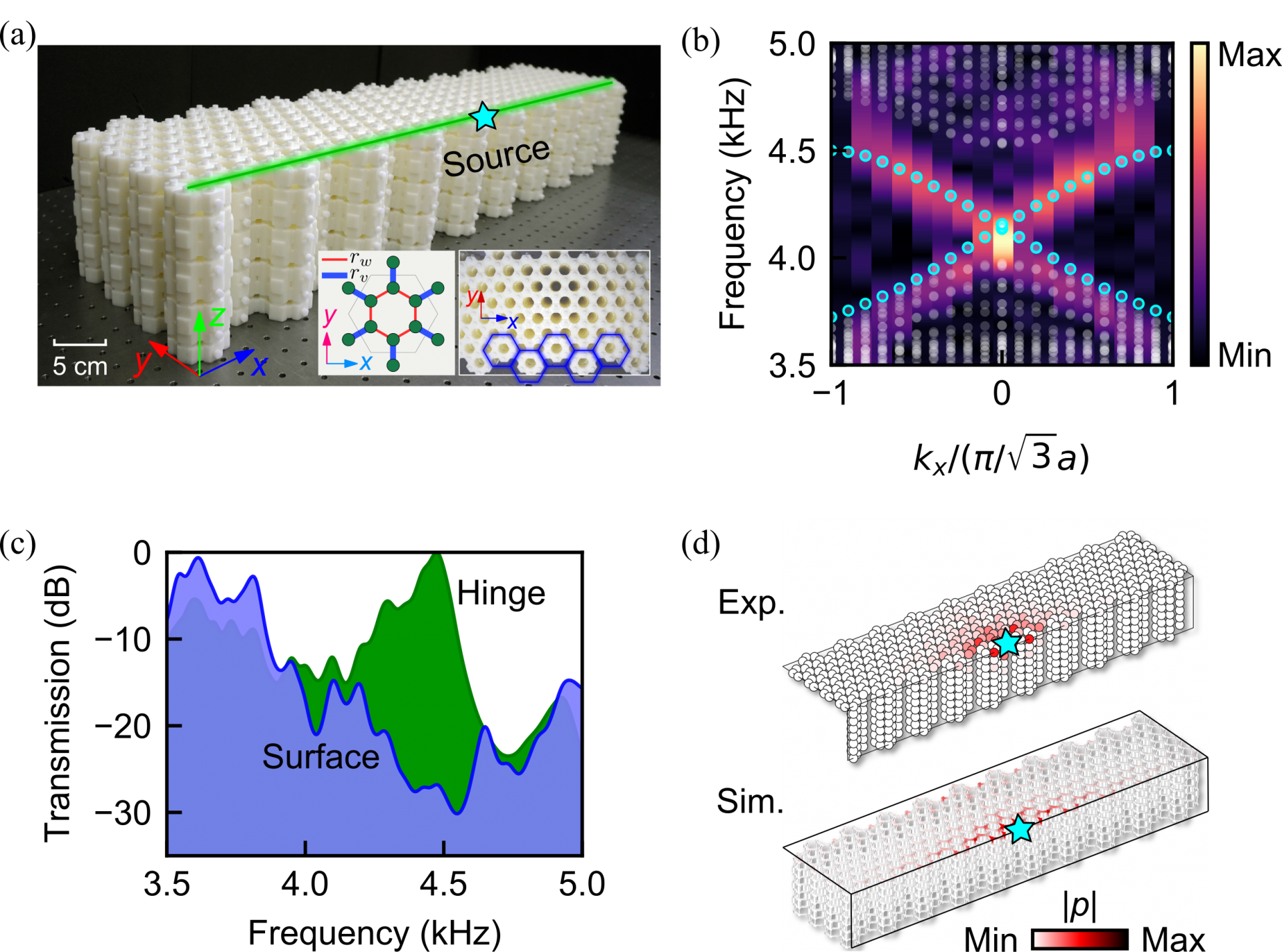
图 4：(a)二阶三维声学拓扑绝缘体样品。(b)二重简并拓扑棱态狄拉克锥实验及仿真结果。(c) 拓扑表面态和拓扑棱态的实验传输谱。 (d) 拓扑棱态声压分布实验和仿真结果。

图4 (a) 展示了二阶三维声学拓扑绝缘体样品，它由图2 (a)的一阶三维声学拓扑绝缘体引入层内对称性破缺得到。层内对称性破缺以后，拓扑表面态的简并狄拉克锥被打开，得到具有两重简并狄拉克锥的拓扑棱态。图4 (b) 中实验测得的棱态狄拉克锥证实了这一预测。图4 (c) 给出了3.5到5.0 kHz范围内拓扑表面态和拓扑棱态传输谱测量结果，可以看到表面态在4.0到4.6 kHz之间具有传输陷带，但是拓扑棱态在拓扑表面态带隙频率范围内保持较高传输率。图4 (d) 给出了4.2 kHz 频率处的声压分布实验和仿真结果，均显示拓扑棱太沿三维声学绝缘体的棱传输。

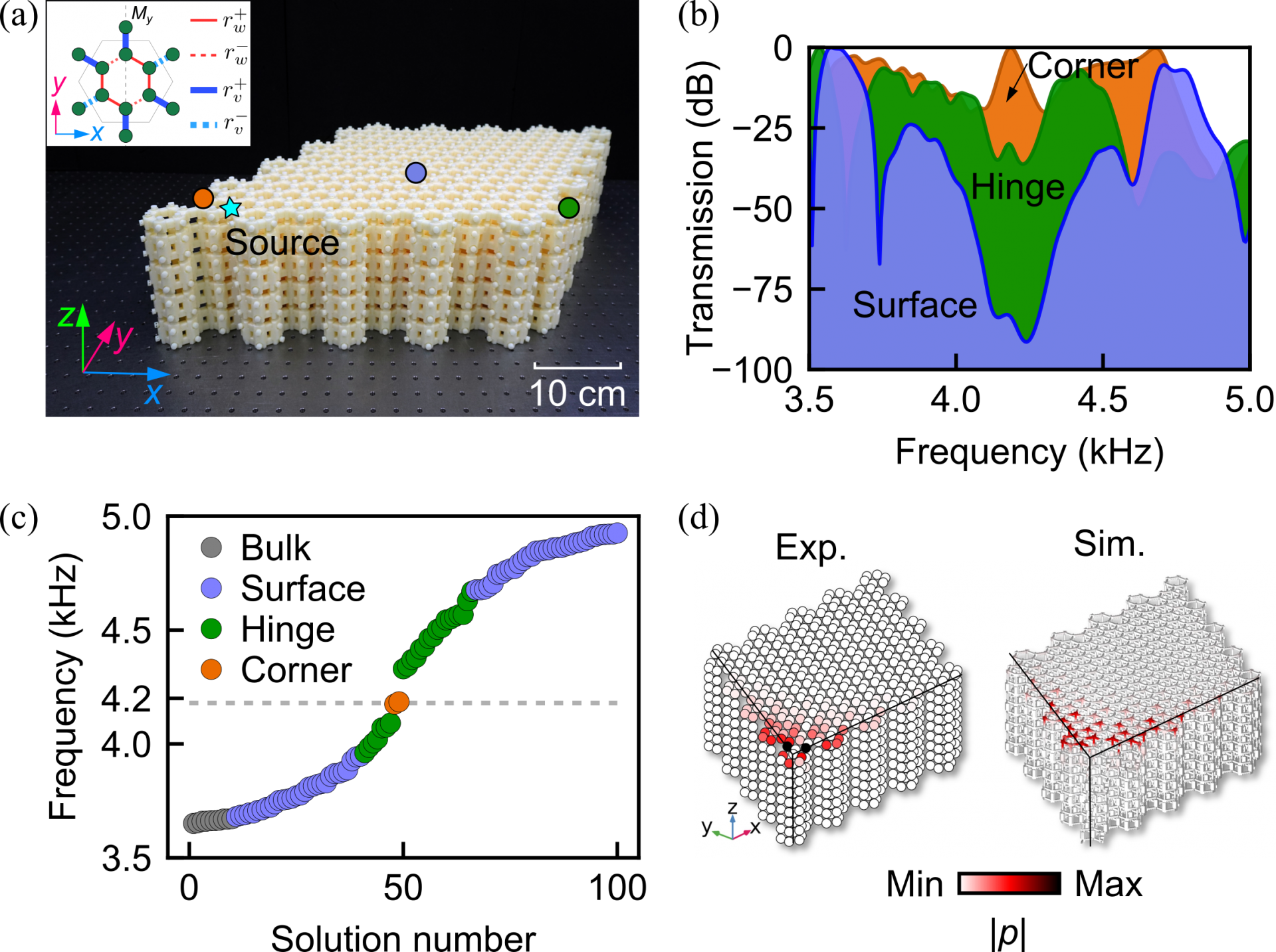
图 5：(a) 三阶三维声学拓扑绝缘体样品。(b) 拓扑表面态、棱态和角态实验传输谱。(c) 三阶三维声学拓扑绝缘体的本征频率计算结果。 (d) 拓扑角态声压分布实验和仿真结果。 

图5 (a) 展示了三阶三维声学拓扑绝缘体样品，它由图4 (a)的二阶三维声学拓扑绝缘体进一步引入层内的镜像对称性破缺得到。此时拓扑棱态的二重简并狄拉克锥也被打开，在两条棱的交点处存在局域化的三阶拓扑角态。图5 (b) 给出了3.5到5.0 kHz范围内的拓扑表面态、棱态和角态传输谱测量结果，可以看到拓扑表面态在4.0到4.6 kHz之间具有很大衰减（蓝色），棱态在此范围具有较高的传输率但在拓扑棱态带隙内仍然存在衰减（绿色），拓扑角态在拓扑棱态带隙内则保持极高的传输率（橙色）。图5 (c) 给出了三阶声学拓扑绝缘体本征频率分布：体态带隙范围内存在表面态、表面态带隙内存在棱态、棱态带隙中存在角态，这也是三阶拓扑绝缘体的典型特征。图5 (d) 给出了4.18 kHz 频率处拓扑角态声场分布的实验和仿真结果，显示了拓扑角态的局域特性。

南科大电子与电气工程系博士后杨林运为论文第一作者，江苏大学物理与电子工程学院研究生王垠为论文共同第一作者，南方科技大学电子与电气工程系高振副教授、浙江大学信息与电子工程学院杨怡豪研究员、江苏大学物理与电子工程学院孙宏祥教授和新加坡南洋理工大学物理与数学科学学院博士生刘癸庚为论文共同通讯作者，南科大为论文第一完成单位。该研究工作得到了国家自然科学基金委和南方科技大学等单位的大力支持。

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.125502 

供稿：电子与电气工程系

通讯员：李佰英

主图：丘妍

编辑：朱增光