近日，南方科技大学电子与电气工程系高振副教授课题组联合中国和新加坡多家单位的合作研究成果，宣告了首个三维陈绝缘体的实验实现。研究成果以“三维光子晶体中的拓扑陈矢量”（Topological Chern vectors in three-dimensional photonic crystals）为题发表在国际顶级期刊Nature上。

1980年，德国科学家冯·克利青首次发现了量子霍尔效应，标志着拓扑物理学的正式诞生。时至今日，拓扑物理学发展已逾四十载，其相关成果三次获得诺贝尔物理学奖。拓扑本是一个数学概念，指的是几何物体在形状连续变化下保持不变的性质。例如，在不进行割断或粘合，只进行伸缩和扭曲的情况下，一个球体可以变成一个正方体，虽然二者形状不同，但他们是拓扑等价的。与此相反，一个球体无法通过连续变化变成一个甜甜圈形状的几何体，因为甜甜圈中间的孔洞只能通过割断或粘合来形成，因此他们是拓扑不等价的。

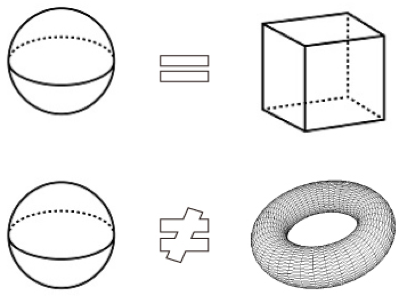
图1球体和正方体拓扑等价，球体与甜甜圈形状几何体拓扑不等价

为了解释一系列量子霍尔效应的实验现象，人们第一次将拓扑这一抽象数学概念运用到物理学当中，诞生了拓扑物理学这一前沿研究领域。人们发现，量子霍尔效应之所以产生，是因为它存在手性边缘态。而手性边缘态的产生，正是源于电子的本征态在动量空间中的拓扑性质。动量空间可以看成是一种特殊的几何体。电子的本征态在动量空间这个几何体上同样也具有拓扑性质。因此，拓扑学的一系列概念，可以直接用来描述电子本征态的拓扑性质。材料拓扑性质的发现，为我们认识材料、发现材料乃至于创造材料提供了全新的自由度。

过去四十余年，科学家们发现了无数拓扑态。其中最基础也最重要的当属量子霍尔家族。该家族最典型的三个成员包括量子霍尔效应、量子反常霍尔效应以及量子自旋霍尔效应。其中量子霍尔效应和量子自旋霍尔效应在实验上发现较早，它们首先在二维体系中被发现，随后很快被扩展到三维系统。相比之下，尽管量子反常霍尔效应理论提出极早（1988年），但由于其实验难度极大，其实验发现却最晚。直到2013年，薛其坤院士团队才首次在实验上观测到量子反常霍尔效应，如图二所示。如果一个体系拥有量子反常霍尔效应，通常又被称为陈绝缘体（Chern insulator），原因在于这个体系的拓扑能带拥有非零的陈数。陈数是描述能带拓扑性质最重要的参数，它也是借用了数学大师陈省身先生在拓扑学中创造的概念。在过去十年间，陈绝缘体相继在不同体系被发现。然而，它们都只局限于二维体系。相比于三维量子霍尔效应和三维量子自旋霍尔效应的蓬勃发展，三维陈绝缘体尚未在任何体系中被发现。

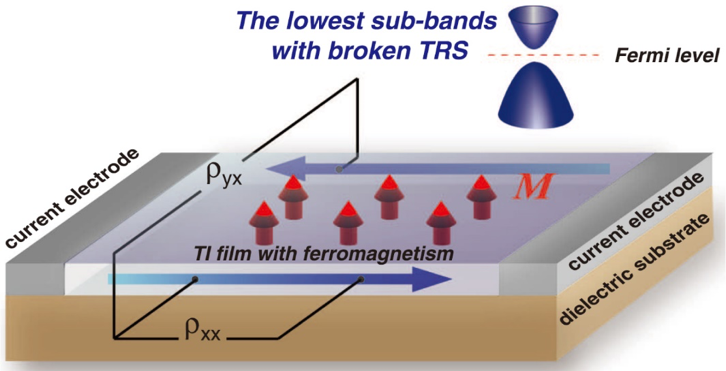
图2 凝聚态体系首个二维陈绝缘体（薛其坤院士团队重大研究成果）

实际上，陈绝缘体不仅存在于凝聚态体系中，也可能存在于经典波体系中。例如，早在2009年，麻省理工学院Marin Soljačić教授课题组便首先在磁性光子晶体中实现了二维光学陈绝缘体，并观测到了单向拓扑边界态。此后，探索经典波体系中的拓扑态便成为拓扑物理学的一个重要分支。这一研究方向根据实验体系不同又可分为拓扑光学、拓扑声学等。研究经典波体系中的拓扑态主要有两方面的意义。首先，从物理角度来讲，经典波体系中人工晶体的加工制备及实验表征难度通常较小，能比较容易的验证一些理论预测的新颖拓扑态。其次，从应用角度来讲，人工晶体的拓扑性质可以为我们调控电磁波、声波等经典波提供全新自由度，进而创造出一系列新颖的光学、声学等器件。

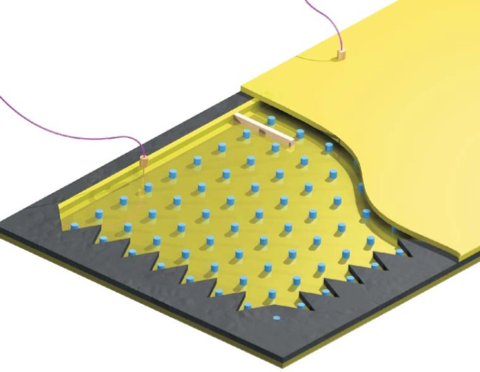
图3光学体系首个二维陈绝缘体（Marin Soljačić教授团队研究成果）

截至目前，陈绝缘体的实现依旧局限在二维体系，三维陈绝缘体的实现对于凝聚态体系仍极为困难。然而，得益于拓扑光学的蓬勃发展，我们却有可能先一步在光学体系中实现三维陈绝缘体。基于此背景，来自新加坡南洋理工大学的张柏乐教授和Chong Yidong教授领导的研究小组，首次在三维磁性光子晶体中实现了三维陈绝缘体，率先将陈绝缘体的研究推进三维时代。

三维磁性光子晶体可以通过堆叠二维磁性光子晶体并引入层间耦合得到。实验样品如图4所示。实验中，将整个样品置于z方向的均匀磁场中以打破时间反演对称性。当我们调节外加磁场的强度，三维磁性光子晶体就会依次表现出三种不同的拓扑态：拓扑平庸态、理想外尔半金属态和三维陈绝缘体态。

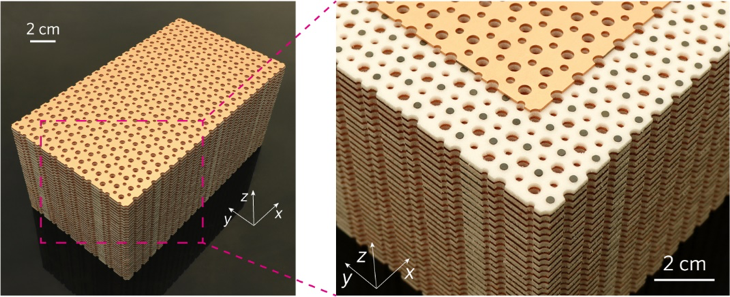
图4 实验加工的三维光学陈绝缘体，右图为局部放大图

其中的拓扑平庸态可以理解为传统意义上没有拓扑性质的普通绝缘体。然而，理想外尔半金属的出现却是一个惊喜。在第一布里渊区中，理想外尔半金属的两个能带之间通过有且只有一对外尔点相连接，它是理论上最理想、最简单的一种外尔半金属。值得一提的是，理想外尔半金属在其他体系中的实现也极为困难。直到2021年，中国科技大学潘建伟院士研究团队才首次在冷原子体系中观测到这种单对的理想外尔点。然而，由于实验体系限制，他们并没有观测到理想外尔半金属的另一个重要特征——单条费米弧表面态。

在本项工作中，利用三维磁性光子晶体的特性，研究者可以直接通过电磁近场扫描获得表面态的等频面（类似于电子体系中费米面）。实验结果如图5所示。不加磁场时，带隙中没有表面态，对应拓扑平庸态。当磁场强度为0.2 T时，可以观测到单条费米弧表面态。这是单条费米弧首次被实验发现。增大磁场到0.35 T，两个外尔点往布里渊区边界方向移动。继续增加磁场，这一对具有相反拓扑荷的外尔点相互湮灭，从而将三维磁性光子晶体从拓扑半金属相变成拓扑绝缘体，诞生了一个全新的拓扑态——三维陈绝缘体。不同于外尔半金属的费米弧（Fermi arc）表面态，三维陈绝缘体的表面态拥有贯穿整个表面布里渊区的费米环（Fermi loop）表面态。这种费米环表面态同样具有手性特征，能沿着某个方向上始终保持单向鲁棒传输。

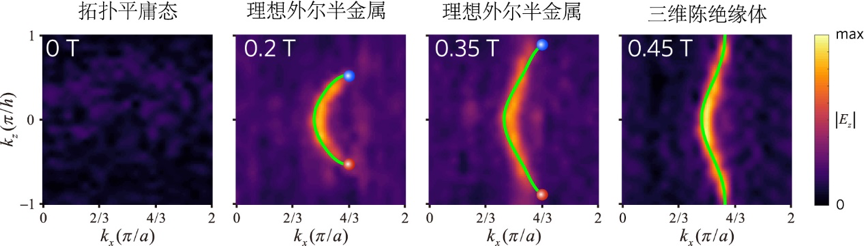 图5 不同磁场强度下仿真和实验获得的拓扑手性表面态

对于二维陈绝缘体，一个陈数便足以描述其能带的拓扑性质。然而，对于三维陈绝缘体，需要用由三个陈数构成的陈矢量来描述。陈矢量具有大小和方向两个特征。实验中，研究者通过调节光子晶体的层间耦合，构造超晶胞，来实现对陈矢量大小的调控。不同陈矢量对应的超晶胞和费米环表面态如图6所示。理论上，通过这种方法，可以获得数值上任意大的陈矢量。

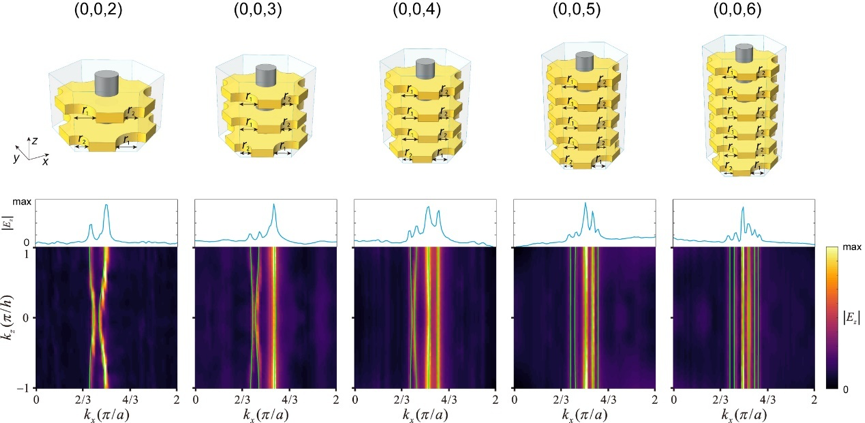
图6 不同大小陈矢量所对应的晶体元胞及拓扑表面态等频面

更加有趣的是，陈矢量的方向可以通过直接转动整个样品轻松实现。陈矢量的方向性在过去的研究中并没有引起足够重视。然而在本项工作中，研究者发现，对于两个三维陈绝缘体之间的表面态，如果它们的陈矢量方向正交，则费米环表面态可以在动量空间中形成复杂且有趣的纽结或者链环。

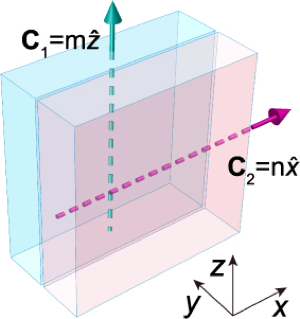
图7 两个陈绝缘体的陈矢量方向正交

对于图7中的两个三维陈绝缘体，陈矢量的大小分别为m和n，但是陈矢量的方向相互正交。在它们的交界面，费米环表面态在表面布里渊区的形状与m和n的取值有关。巧合的是，拓扑学里有个名叫纽结理论（knot theory）的数学分支便是专门研究这种结构的。根据数学上的结论，我们可以得知，如果m和n互质，则费米环表面态会形成独立纽结。相反，如果m和n不互质，则会形成多个纽结嵌套在一起的链环，且纽结个数为m和n的最大公约数。图8展示了对于不同陈矢量的组合，费米环表面态在表面布里渊区的投影。由于纽结和链环的形成是由陈矢量决定的，因此它们的结构也是受到拓扑保护的，能够极其稳定的存在，未来可能用于拓扑计算等领域。

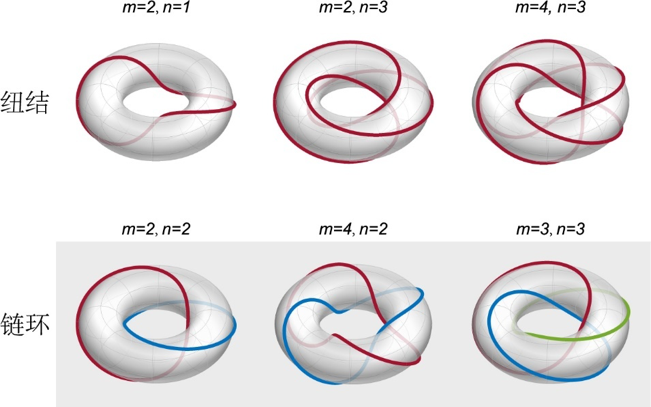
图8 对于不同陈矢量的组合，费米环表面态可以在表面布里渊区形成纽结或者链环

实验上，研究者研究了m=2，n=2的情况。实验装置和结果如图9所示。可以看出，在两个三维陈绝缘体交界面的布里渊区上，有两个独立的费米环相互嵌套在一起形成了一个纽结理论中最简单的链环——Hopf link。

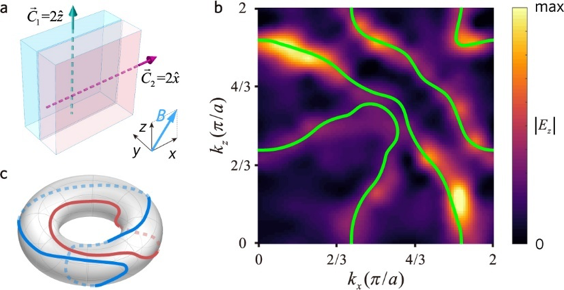
图9陈矢量m=2，n=2对应的费米环表面态形成的Hopf link

该工作标志着陈绝缘体正式进入三维时代。从基础物理层面讲，这一寻找多年的拓扑态终于被实验发现，极大地扩充了拓扑家族的成员。此外，数学体系中的纽结与链环概念首次在物理体系中被实验观测到，极大地加强了数学拓扑与物理拓扑之间的内在联系。从实际应用层面讲，三维陈绝缘体的手性拓扑表面态具有受拓扑保护的单向、鲁棒传输特性，可对任何缺陷、杂质、无序、尖锐拐角等障碍免疫而具有绝对鲁棒性。未来无论是大容量、高效率、低损耗电磁信息传输还是拓扑计算，三维陈绝缘体都将是一个不可或缺的重要成员。得益于光学体系的优异特性，这项工作不仅实验验证了一系列过去的理论预言，而且发现了一些过去理论层面尚未触及到的新奇物理现象。同时，我们也期待三维陈绝缘体能够在凝聚态体系中尽早被发现，将拓扑家族成员进一步完善。

南洋理工大学博士生刘癸庚和高振为共同第一作者，南洋理工大学教授张柏乐、Chong Yidong，浙江大学研究员杨怡豪和电子科技大学教授周佩珩为共同通讯作者。南科大为论文共同第一单位。以上研究得到了国家自然科学基金委员会、南方科技大学以及新加坡教育部门的支持。

 论文链接：https://www.nature.com/articles/s41586-022-05077-2 

供稿：电子与电气工程系

通讯员：李佰英

主图：丘妍

编辑：朱增光