近日，南方科技大学数学系2019级本科生魏元哲与其学术导师吴开亮副教授、阿拉巴马大学助理教授孙铮，合作在龙格-库塔（Runge-Kutta）方法的稳定性研究方面取得重要成果。该研究成果以题为“On Energy Laws and Stability of Runge-Kutta Methods for Linear Seminegative Problems”在计算数学领域著名期刊SIAM Journal on Numerical Analysis正式发表。魏元哲证明了论文中具有挑战性的定理5.1（解析构造并证明了一族复杂正定矩阵的Cholesky分解），从而推导出任意阶对角Padé逼近的离散能量恒等式。

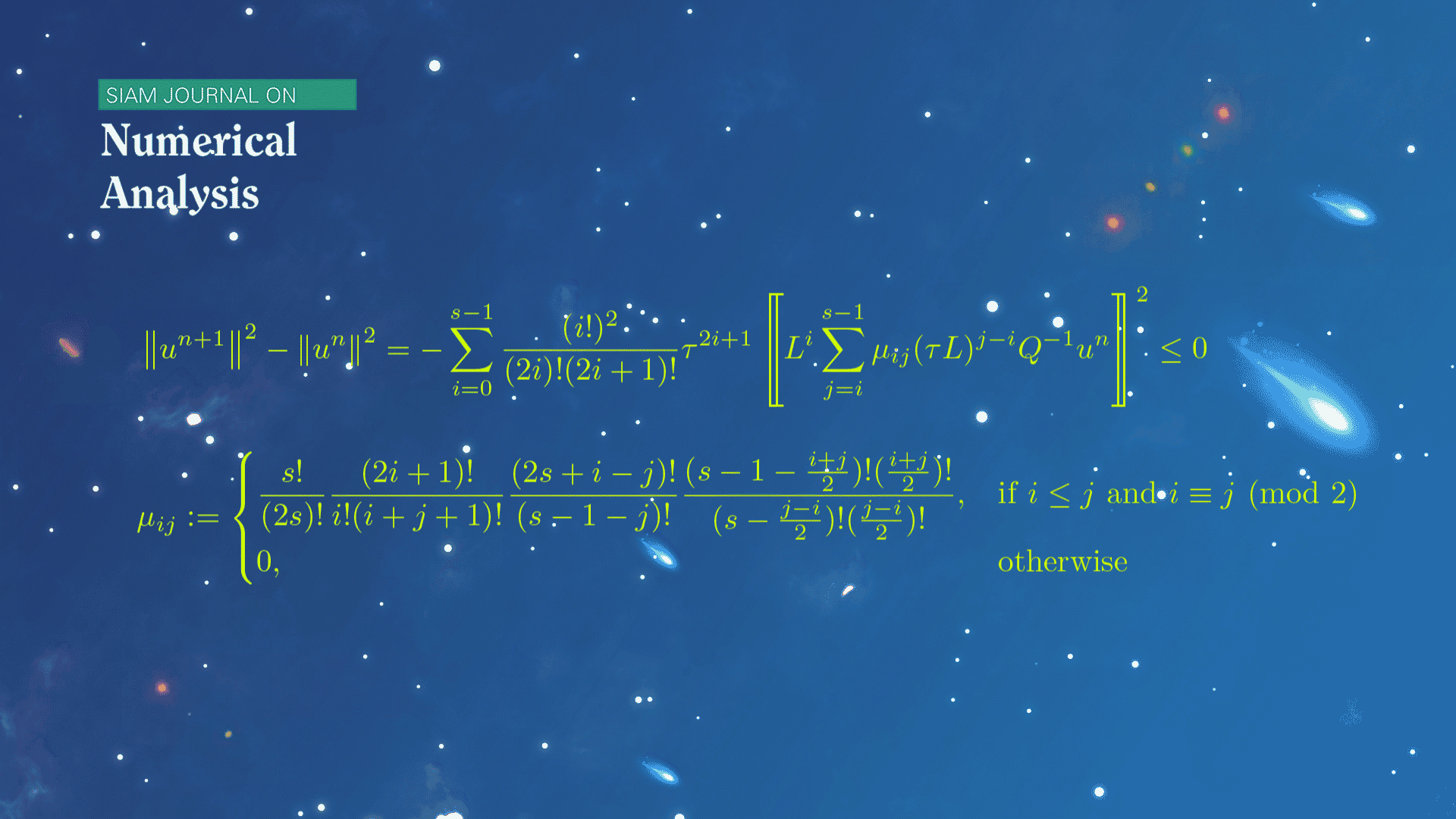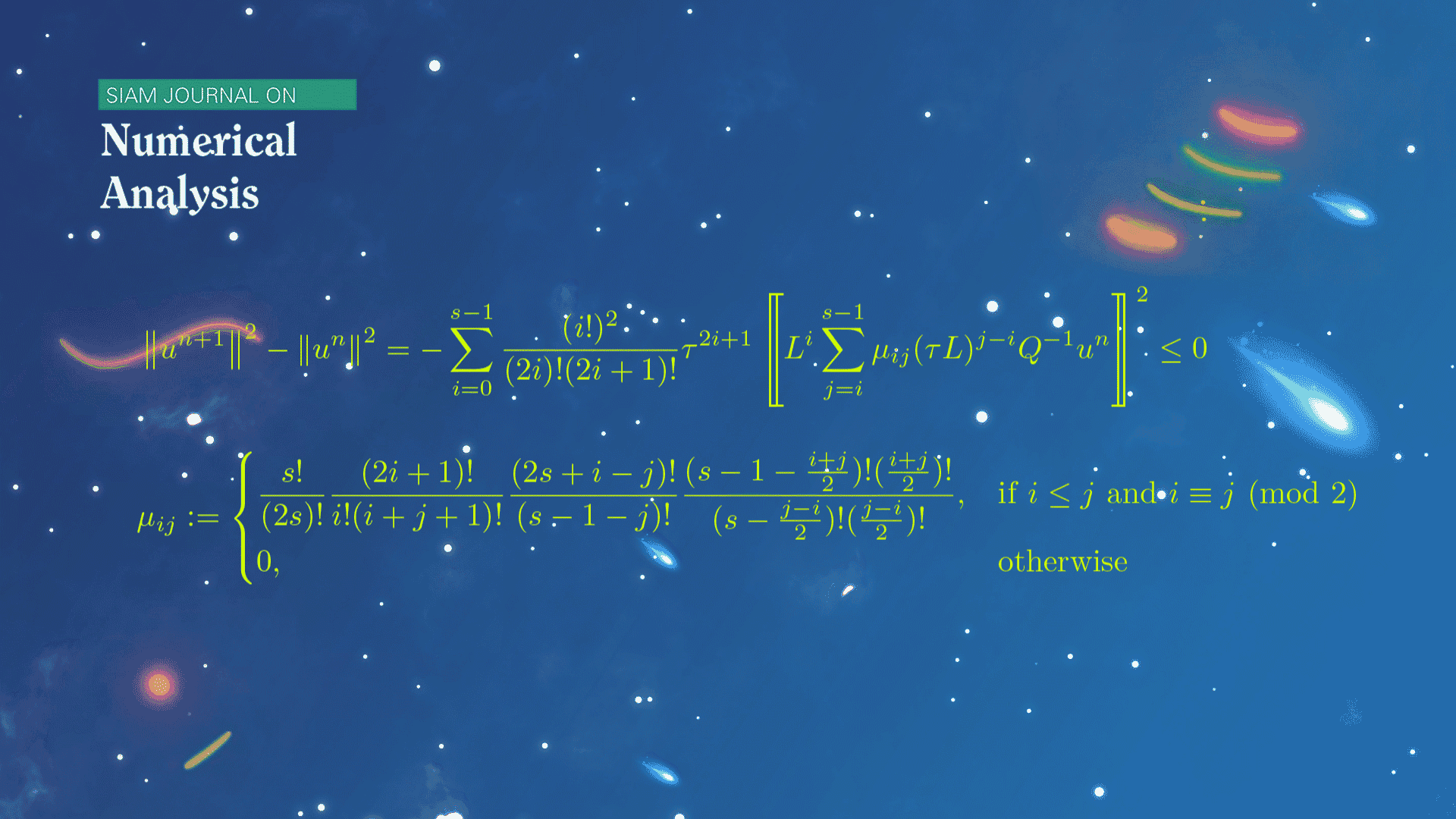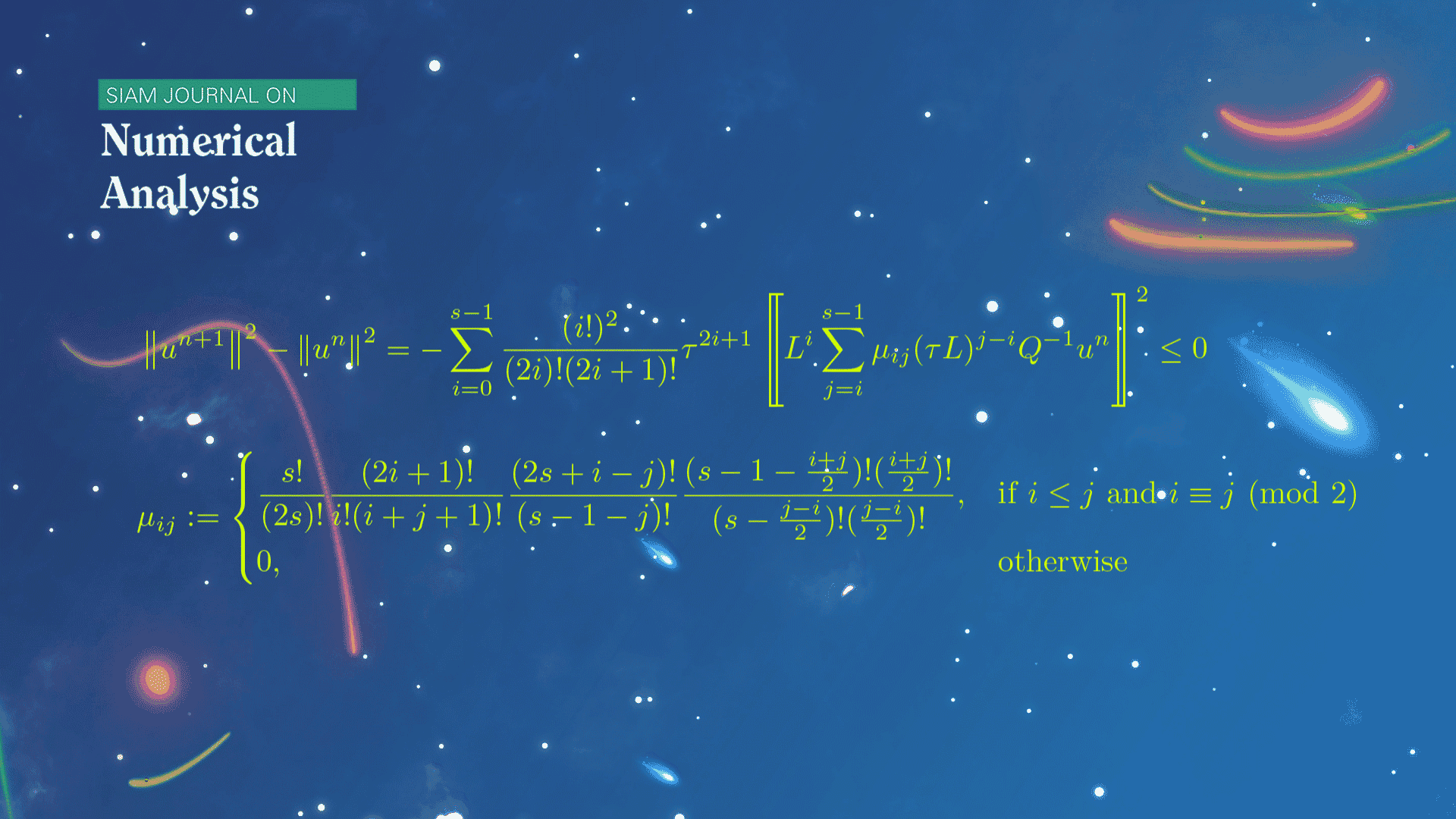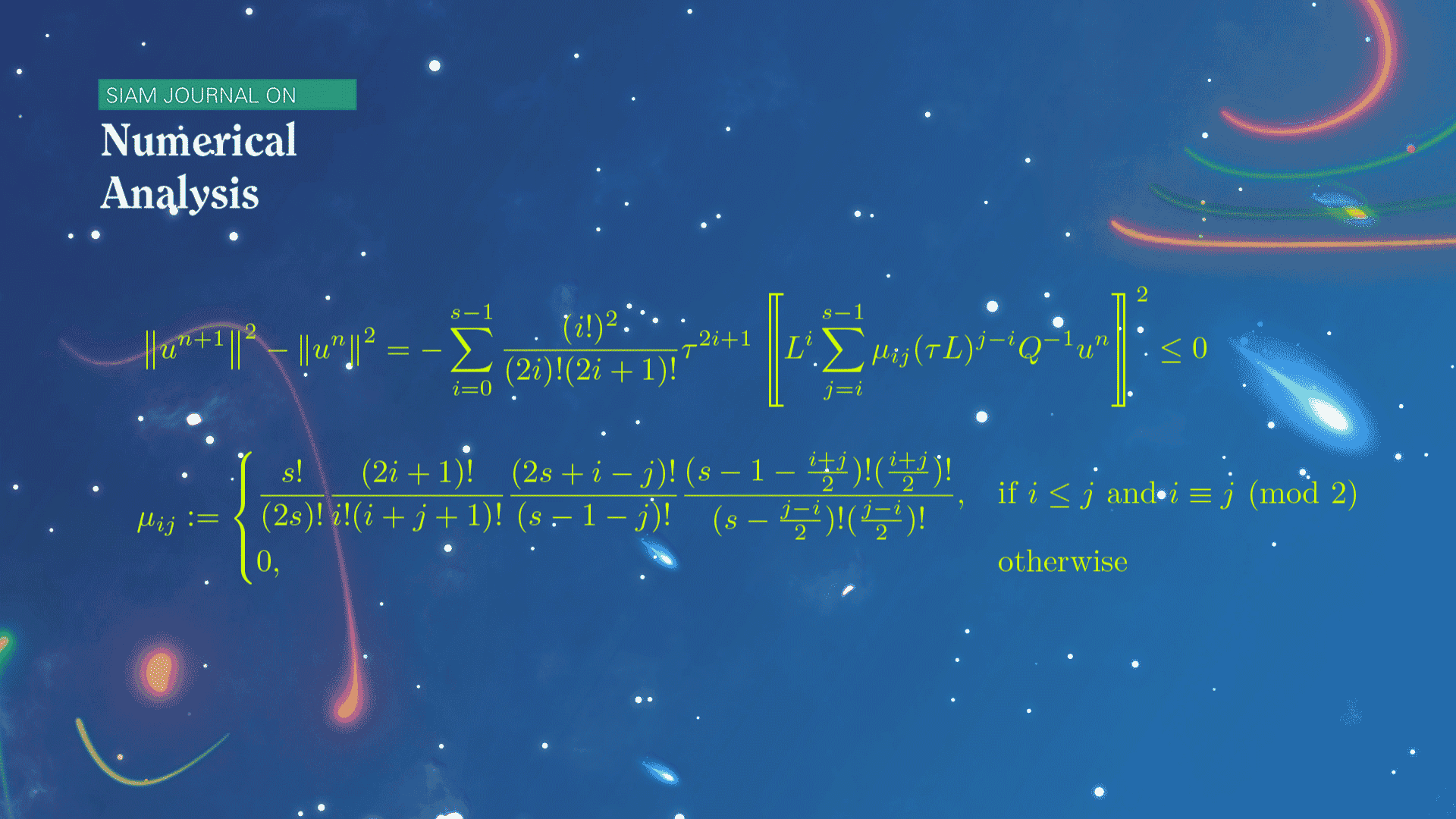
龙格-库塔方法是数值求解微分方程（组）的一类重要算法，已被广泛应用于科学与工程领域，算法的稳定性对数值计算结果有决定性的影响。长期以来，对龙格-库塔方法稳定性的理解和刻画是数值分析领域的重要基本问题之一，该方面研究受到了许多计算数学家的关注，形成了诸多经典的理论，例如基于线性标量Dahlquist方程的稳定性区域理论、对非线性系统的代数稳定性理论等。

该论文聚焦于一般的线性半负定系统，从新的角度研究了龙格-库塔方法给出的数值解的能量演化规律。受到分部积分技巧和连续系统能量耗散规律的启发，该论文建立了推导一般的显式或隐式的龙格-库塔方法离散能量恒等式的理论框架，由此给出了龙格-库塔方法的强稳定性和弱稳定性的判定准则。论文中还详细阐述了对角Padé逼近对应的一类龙格-库塔方法，基于超几何级数技术和若干巧妙的组合恒等式，建立了任意阶此类方法的一般能量恒等式。此离散能量恒等式与连续问题的能量恒等式的一种开展形式具有类似的结构，揭示了连续和离散能量演化规律之间的内在联系。

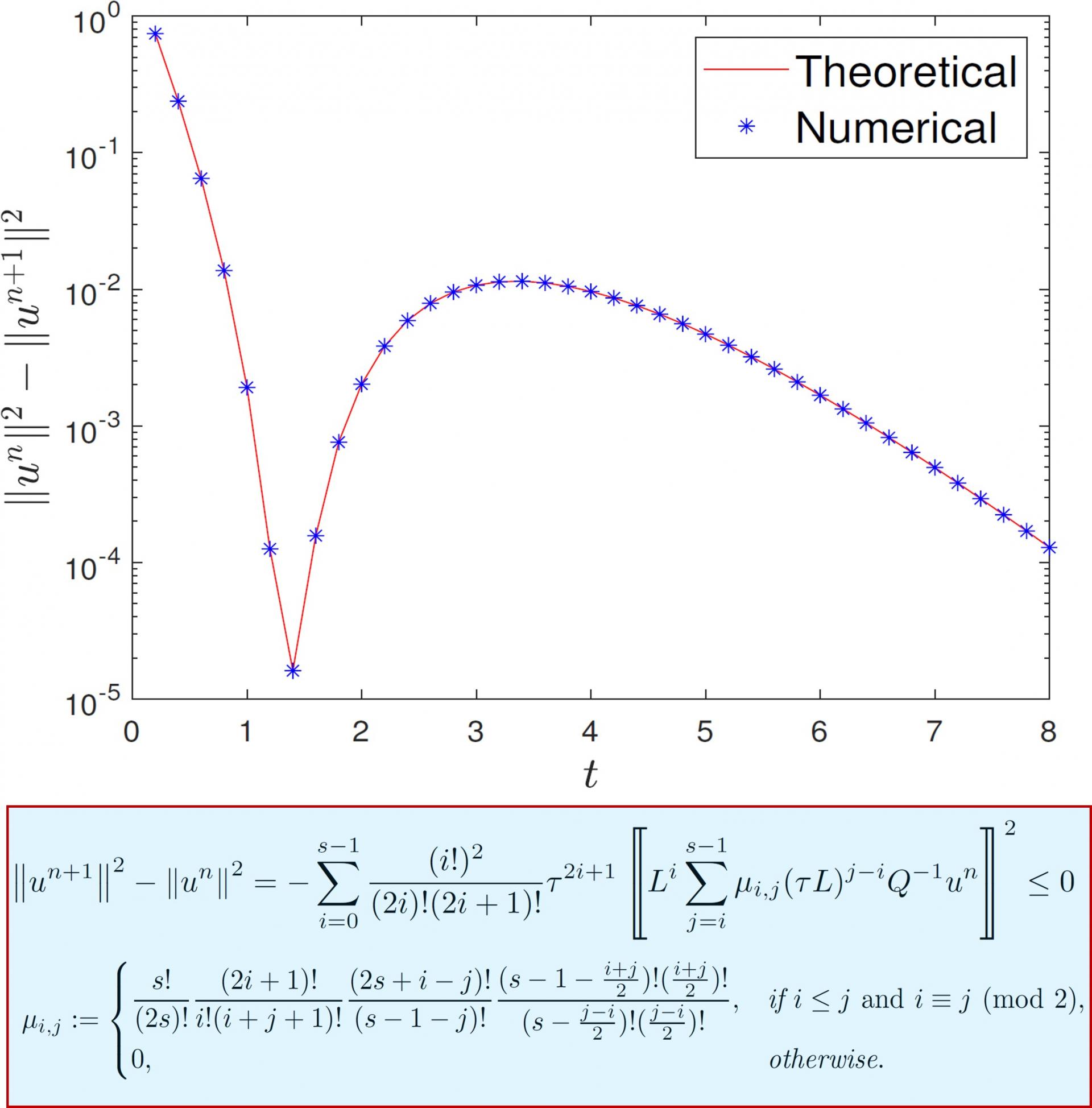
图1.对角Padé逼近对应的离散能量恒等式

魏元哲、吴开亮、孙铮为该论文共同一作，吴开亮为通讯作者，南科大为论文唯一通讯单位。

论文链接：https://epubs.siam.org/doi/10.1137/22M1472218 

供稿：数学系

通讯员：卢圣红

主图：丘妍

编辑：朱增光