近日,南方科技大学量子科学与工程研究院副研究员吴健生与研究员孔良两个课题组合作,从理论上阐述了完备描述拓扑序的物理量的普适实验测量方案,并以ToricCode为例,在实验中测量了Toriccode拓扑序的基本数据。该研究以“Uniquely identifying topological order based on boundary-bulk duality and anyon condensation”为题,在我国顶级英文科学期刊《国家科学评论(National Science Review)》发表,本论文作为封面文章发表并配了封面图案。
拓扑序是一种超越朗道对称性破缺理论的新量子物态,其特征包括简并的基态、长程量子纠缠和任意子。对拓扑序的刻画和探测是凝聚态物理领域的重要问题,并且是拓扑量子计算的基础。任意子(anyon)是二维拓扑序中具有分数统计的准粒子激发。在分数量子霍尔效应系统中利用输运测量等实验手段探测任意子是近年来备受关注的研究课题。数学上证明,任意子的编织(braiding)和融合(fusion)是能够完备描述拓扑序的物理量,分别由R-矩阵和F-矩阵表示。但是在实验上如何对这些数据进行测量是一个非常有挑战性的难题。

简单解释一下这两类矩阵。考虑图1(a)所示的两个过程:1.直接融合任意子a和b,产生任意子c;2.先交换a,b的位置(编织),再融合产生c。两个过程得到的任意子类型相同,但其拓扑波函数相差一个变换,即R-矩阵。图1(b)展示了任意子a,b,c的两种融合顺序,它们最终的任意子类型相同,但中间的任意子i和 j存在不同的可能性。两种不同的融合方式之间的变换矩阵就是F-矩阵。R-矩阵和F-矩阵是完备描述拓扑序的基本物理量,却一直没有有效的测量方案。它们的测量存在两个困难:一个是在格点模型中,a和b两个任意子交换位置前后,除了我们需要的波函数的变化(即R-矩阵)之外,还有两个任意子相对位置的不同(见图c中),一般方法不能只测波函数部分的变化;另外一个困难是:R-矩阵不是唯一的,它有不同的规范等价的数据,似乎不是一个可测量的物理量。
课题组成员通过Toric code模型对这一问题进行了探索。发现:可以通过拓扑态的体态-边界态的对应关系和任意子在边界上的凝聚来解决上面两个困难。当模型存在边界时,一些任意子在边界上等价于真空,可以被局域地产生和湮灭;而另一些会留在边界上,成为边界任意子。课题组设计这样的过程:让任意子在边界上产生,然后与另外的任意子交换位置,然后又消失在边界上。通过这样的过程,任意子实现了交换,同时初态和末态的空间位置又没有不同,这样解决了第一个困难。这样也证明了利用边界的性质,交换任意子的效应可以在边界上通过半编织(half-braiding)过程得到,即:体态任意子可以由具备半编织(half-braiding)的边界任意子定义(图2b);同时边界的半编织定义了体态中的编织(图2b,c),而前者可以通过实验直接测量。此外发现,不同的规范等价R-矩阵可以由不同类型边界上的半编织得到,这样又解决了第二个困难。
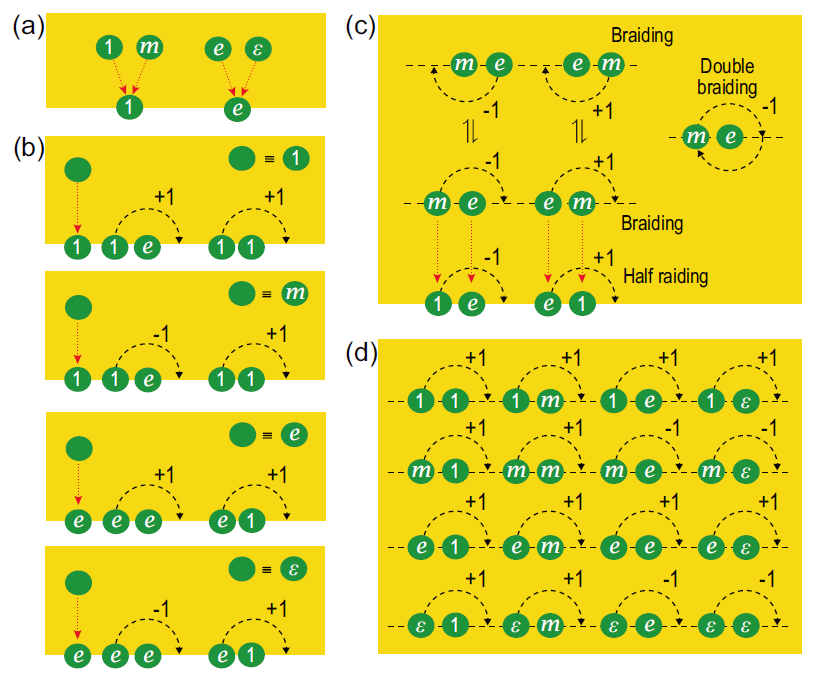
另一方面,F-矩阵能够通过测量不同融合顺序的量子态得到。课题组成员利用核磁共振量子处理器对测量方案进行了原理性实验演示。实验测量了Toric code模型中m和e任意子的非平庸编织,以及一个F-矩阵元。该工作是拓扑序刻画和测量的基础性研究,测量了完备确定拓扑序的最基本物理量,也将对未来拓扑序在量子计算中的应用带来启示。
南科大是论文第一单位。南科大量子科学与工程研究院研究生海咏菊、物理系博士生张泽为论文共同第一作者,吴健生与孔良为共同通讯作者,俞大鹏院士为最后作者。该研究工作得到了广东省科技厅、深圳市科创委、国家自然科学基金委和南方科技大学等部门的大力支持。
论文链接:https://doi.org/10.1093/nsr/nwac264
供稿: 量子科学与工程研究院
通讯员:赵若云
主图:丘妍
编辑:朱增光




