近日，南方科技大学物理系、量子科学与工程研究院教授卢海舟团队在三维霍尔效应理论方面取得重要进展，相关成果以“Theory for the Charge-Density-Wave Mechanism of 3D Quantum Hall Effect”为题在《物理评论快报》(Physical Review Letters) 发表[1]。该成果被选为编辑推荐并被美国物理学会作为Physics杂志Viewpoint推介。

1980年，量子霍尔效应的发现成为了物理学史上最激动人心的篇章之一。量子霍尔效应表现为，在非常低的温度和非常高的磁场下，霍尔电阻量子化为h/e2的整数倍[2]（h是普朗克常数，e是电子电量）。此后，物理学家们还发现了如量子反常霍尔效应等不需要磁场的版本[3]。在量子霍尔效应被发现的这几十年，已经诞生了3个诺贝尔物理学奖，与之相关的拓扑物态也成为物理学的重要研究方向。

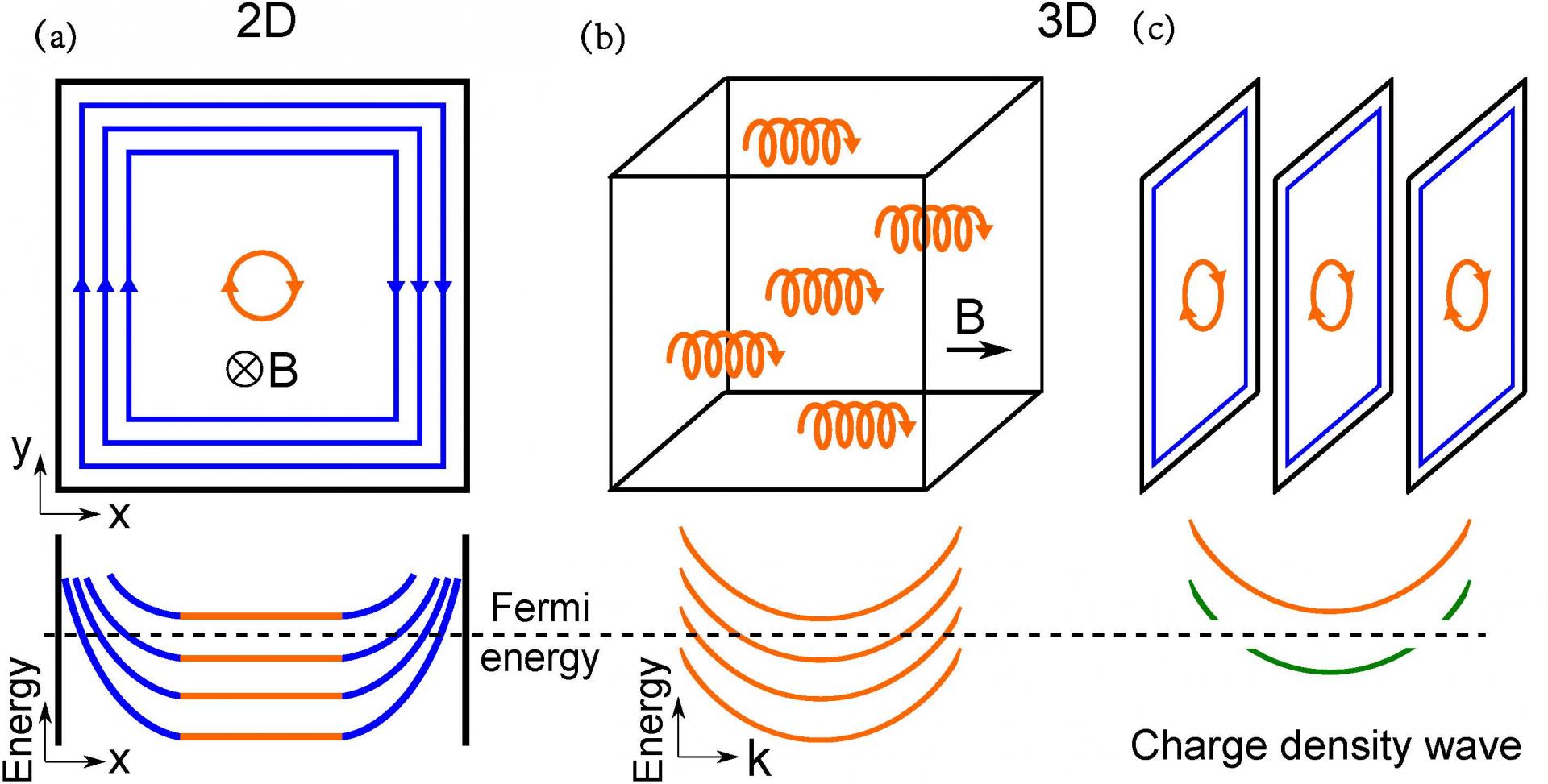
(a)在二维体系中，量子霍尔效应出现时，只有边缘态(蓝色)传导电子，而内部体态是绝缘的，因为费米能量位于朗道能级之间。(b)在三维，朗道能级成为沿着磁场方向色散的一维朗道能带。量子霍尔效应在三维中很难实现，因为费米能量总要穿过一些朗道能带，所以体态是金属的。(c)电荷密度波可以打开朗道能带的间隙，从而使体态绝缘，可以观察到量子霍尔效应。该图引用自文献 [1]

早期的研究认为量子霍尔效应很难在三维体系中实现[4-7]，物理学家30年来一直在追求量子霍尔效应的三维版本，但一直没有得到令人信服的结果。直到2019年，南科大的张立源团队成功在化合物ZrTe5上观测到三维量子霍尔效应[8]。张立源团队使用高迁移率低电子浓度的高质量样品，冷却到0.6开尔文，在大小为1.7到2.1特斯拉的磁场范围间观察到了量子化的霍尔电阻平台和0纵向电阻率。在这个实验中，电荷密度波被认为是最有可能的机制。电荷密度波是个关联效应，可以把一个三维系统分成多层的二维量子霍尔效应的叠加。

此时，物理学家对这些新结果产生了新的困惑：观测到的三维量子霍尔效应背后的定量物理机制是什么？为什么霍尔平台只存在于一定的磁场范围内？南科大卢海舟团队提出了新的理论以解决这两个问题[1]。在研究团队的模型中，一个磁场诱导的电荷密度波可以用来解释三维量子霍尔效应平台。他们发现，磁场引发了基于电子-声子相互作用的从正常态到电荷密度波态的二级相变。此外，磁场中同时存在公度和非公度两种电荷密度波，且在1.7-2.1特斯拉之间公度电荷密度波基态能量更低，从而解释了此段磁场的霍尔平台，也解释了在2.1特斯拉以上没有霍尔电阻平台的困惑。

在上世纪，物理学对世界的认识很大程度上基于对称性破缺的有序相变，而在本世纪，拓扑相变逐渐成为探索新物理的世界观。本研究探索了一种连接两个世纪的罕见情况，即同一个磁场在一个方向上诱导有序相变，但在另外两个方向上诱导拓扑相变。

南科大校长卓越博士后覃昉为该文章的第一作者，卢海舟是通讯作者，合作者包括南科大物理系教授张文清，量子科学与工程研究院院长、物理系讲席教授、中国科学院院士俞大鹏，北京大学教授、中国科学院院士谢心澄。

该项目获得了国家自然科学基金、科技部重点研发计划、中科院战略优先研究计划、广东省普通高校创新团队、深圳市重点实验室、深圳市高水平大学建设亮点项目、中国博士后基金、南方科技大学卓越博士后基金、南方科技大学高性能计算平台、上海自然科学基金的支持。

文章链接: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.125.206601

参考文献

[1] F. Qin, S. Li, Z. Z. Du, C. M. Wang, W. Q. Zhang, D. P. Yu, H. Z. Lu, and X. C. Xie, "Theory for the charge-density-wave mechanism of 3D quantum Hall effect", Phys. Rev. Lett. 125, 206601 (2020). 

[2] K. von Klitzing, et al., "New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance", Phys. Rev, Lett. 45, 494 (1980).

[3] C. Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei, L. L. Wang, Z. Q. Ji, Y. Feng, S. Ji, X. Chen, J. Jia, X. Dai, Z. Fang, S. C. Zhang, K. He, Y. Wang, L. Lu, X. C. Ma, and Q. K. Xue, "Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator", Science 340, 167 (2013).

[4] J. R. K. Cooper, et al., "Quantized Hall effect and a new field-induced phase transition in the organic superconductor (TMTSF)2(PF)6", Phys. Rev. Lett. 63, 1984 (1989).

[5] S. T. Hannahs, et al., "Quantum Hall effect in a bulk crystal", Phys. Rev. Lett. 63, 1988 (1989). 

[6] S. Hill, et al., "Bulk quantum Hall effect in η-Mo4O11", Phys. Rev. B 58, 10778 (1998).

[7] H. Cao, et al., "Quantized Hall effect and Shubnikov-de Haas oscillations in highly doped Bi2Se3: Evidence for layered transport of bulk carriers", Phys. Rev. Lett. 108, 216803 (2012). 

[8] F. Tang, Y. Ren, P. Wang, R. Zhong, J. Schneeloch, S. A. Yang, K. Yang, P. A. Lee, G. Gu, Z. Qiao, and L. Zhang, "Three-dimensional quantum Hall effect and metal-insulator transition in ZrTe5", Nature 569, 537 (2019).

供稿：物理系

通讯员：廖薮祺

编辑：李思颖

主图设计：丘妍